Bicone Calculator
Calculator and formulas for calculating a bicone
Bicone Calculator
The Bicone
The bicone is a double cone consisting of two identical cones joined at their bases.
Bicone Properties
The bicone: Two identical cones joined at their circular bases
Bicone Structure
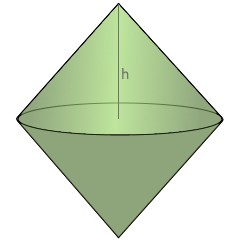
The bicone with perfect double symmetry.
Two cones joined at their common base.
|
|
What is a bicone?
The bicone is a fascinating double rotational solid:
- Definition: Two identical cones joined at their bases
- Common Base: Shared circular base between the cones
- Symmetry: Perfect bilateral symmetry
- Shape: Characteristic hourglass or diamond profile
- Rotation: Rotational symmetry around the central axis
- Structure: Two apex points connected by a circular waist
Geometric Properties of the Bicone
The bicone demonstrates remarkable geometric properties:
Basic Parameters
- Radius (r): Radius of the common circular base
- Cone Height (h): Height of each individual cone
- Total Height: 2h (both cones combined)
- Slant Height (L): √(h² + r²)
Special Properties
- Double Cone: Two identical cones combined
- Perfect Symmetry: Bilateral and rotational
- Common Base: Shared circular foundation
- Hourglass Profile: Characteristic waisted shape
Mathematical Relationships
The bicone follows elegant mathematical laws:
Volume Formula
Exactly twice the volume of a single cone. Simple and elegant relationship.
Surface Formula
Only lateral surfaces, no base area. Internal base is hidden.
Applications of the Bicone
Bicones find applications in various fields:
Technology & Engineering
- Antenna designs
- Optical systems
- Fluid dynamics
- Acoustic devices
Science & Research
- Crystal structures
- Molecular geometry
- Physics experiments
- Mathematical modeling
Education & Teaching
- Geometry lessons
- 3D visualization
- Symmetry studies
- Volume calculations
Art & Design
- Sculptural forms
- Decorative objects
- Jewelry design
- Artistic installations
Formulas for the Bicone
Slant Height (L)
Pythagorean theorem for the slant line
Surface Area (S)
Two cone lateral surfaces, no base area
Volume (V)
Exactly twice the volume of a single cone
Calculation Example for a Bicone
Given
Find: All properties of the bicone
1. Slant Height Calculation
For r = 3, h = 5:
\[L = \sqrt{r^2 + h^2}\] \[L = \sqrt{3^2 + 5^2} = \sqrt{34}\] \[L ≈ 5.83\]The slant height is approximately 5.83 units
2. Surface Area Calculation
For r = 3, L ≈ 5.83:
\[S = 2 \cdot \pi \cdot r \cdot L\] \[S = 2 \cdot \pi \cdot 3 \cdot 5.83\] \[S ≈ 109.96\]The surface area is approximately 109.96 square units
3. Volume Calculation
For r = 3, h = 5:
\[V = \frac{2}{3} \cdot r^2 \cdot \pi \cdot h\] \[V = \frac{2}{3} \cdot 9 \cdot \pi \cdot 5\] \[V = 30\pi ≈ 94.25\]The volume is approximately 94.25 cubic units
4. Double Cone Verification
Single cone volume:
\[V_{single} = \frac{1}{3} \cdot r^2 \cdot \pi \cdot h\] \[V_{single} = \frac{1}{3} \cdot 9 \cdot \pi \cdot 5 = 15\pi\] \[V_{bicone} = 2 \cdot V_{single} = 30\pi ✓\]Verification: bicone volume = 2 × single cone volume
5. The Perfect Bicone
The bicone with perfect double symmetry
The Bicone: Elegance of Double Symmetry
The bicone represents one of the most elegant examples of composite geometric forms, embodying the perfect marriage of symmetry and functionality. Created by joining two identical cones at their circular bases, the bicone demonstrates how simple geometric principles can produce complex and beautiful three-dimensional forms. Its characteristic hourglass or diamond-shaped profile has captivated mathematicians, engineers, and artists for centuries, serving as a fundamental shape in crystallography, antenna design, and decorative arts. The mathematical beauty of the bicone lies in its elegant formulas that simply double the properties of a single cone, yet create an entirely new geometric entity with unique characteristics.
The Geometry of Perfect Symmetry
The bicone demonstrates the power of geometric symmetry:
- Bilateral Symmetry: Perfect mirror symmetry across the central plane
- Rotational Symmetry: Complete 360° symmetry around the central axis
- Common Base: Shared circular foundation hidden within
- Double Apex: Two identical pointed ends
- Hourglass Profile: Characteristic waisted silhouette
- Unified Structure: Single continuous surface
- Mathematical Elegance: Simple doubling relationships
Mathematical Simplicity
Volume Doubling
The bicone volume formula elegantly doubles the single cone volume, demonstrating the additive nature of geometric composition.
Surface Purity
With no exposed base area, the bicone surface consists purely of lateral cone surfaces, creating a seamless form.
Structural Balance
The bicone's perfect symmetry provides structural stability and aesthetic appeal in both natural and engineered forms.
Universal Applications
From crystal structures to antenna designs, the bicone's unique properties make it invaluable across multiple disciplines.
Summary
The bicone stands as a testament to the beauty and functionality of symmetric geometric forms. Its elegant construction from two identical cones creates a shape that is both mathematically pure and practically versatile. The simple doubling relationships in its formulas reflect the additive nature of its construction, while its perfect symmetry provides both structural integrity and aesthetic appeal. From the microscopic world of crystal lattices to the macroscopic realm of architectural design, the bicone continues to inspire and serve as a fundamental building block of three-dimensional geometry. Its timeless form demonstrates how mathematical principles can produce shapes of enduring beauty and practical utility, making it an essential study in the field of solid geometry and a perfect example of how symmetry creates both mathematical elegance and functional excellence.