Truncated Cone Calculator
Calculator and formulas for calculating a truncated cone (frustum)
Truncated Cone Calculator
The Truncated Cone (Frustum)
The truncated cone is a section of a cone with the top cut off parallel to the base.
Truncated Cone Properties
The frustum: Section of cone with parallel circular faces
Truncated Cone Structure
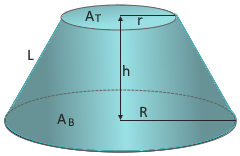
The truncated cone with two parallel faces.
Large base and smaller top circle.
|
|
What is a truncated cone?
The truncated cone (frustum) is a fundamental three-dimensional solid:
- Definition: Section of a cone with the top cut off
- Base: Large circular surface at the bottom
- Top: Smaller circular surface parallel to the base
- Sides: Slanted lateral surface connecting the circles
- Symmetry: Rotational symmetry around central axis
- Applications: Common in engineering and architecture
Geometric Properties of the Truncated Cone
The truncated cone demonstrates elegant geometric relationships:
Basic Parameters
- Small radius (r): Radius of the top circular face
- Large radius (R): Radius of the bottom circular face
- Height (h): Distance between the two circular faces
- Lateral length (L): √((R-r)² + h²)
Special Properties
- Cone section: Part of a complete cone
- Parallel faces: Top and bottom are parallel circles
- Slant surface: Lateral surface connects the circles
- Rotational solid: Symmetric around central axis
Mathematical Relationships
The truncated cone follows elegant mathematical laws:
Volume Formula
Contains R², Rr, and r² terms. Elegant cone section formula.
Surface Formula
Two circular areas plus lateral surface. Pythagorean theorem for slant length.
Applications of the Truncated Cone
Truncated cones find widespread applications across many fields:
Engineering & Manufacturing
- Pipe transitions and reducers
- Funnels and hoppers
- Machine components
- Pressure vessel sections
Architecture & Construction
- Column capitals and bases
- Decorative elements
- Structural transitions
- Roof and dome sections
Everyday Objects
- Buckets and containers
- Lamp shades
- Cups and vessels
- Traffic cones (modified)
Education & Mathematics
- Geometry lessons
- Volume calculations
- Surface area problems
- 3D solid demonstrations
Formulas for Calculating Truncated Cones
Top Surface (AT)
Area of the smaller circular top
Base Surface (AB)
Area of the larger circular base
Lateral Length (L)
Slant height using Pythagorean theorem
Lateral Surface (SL)
Curved surface area of the frustum
Total Surface (S)
Sum of lateral surface and both circular areas
Volume (V)
Volume with three radius terms
Large Perimeter (PL)
Circumference of the large base
Small Perimeter (PS)
Circumference of the small top
Calculation Example for a Truncated Cone
Given
Find: All properties of the truncated cone
1. Surface Areas Calculation
Top and base areas:
\[A_T = r^2 \cdot \pi = 3^2 \cdot \pi = 9\pi ≈ 28.27\] \[A_B = R^2 \cdot \pi = 5^2 \cdot \pi = 25\pi ≈ 78.54\]Top area ≈ 28.27, Base area ≈ 78.54 square units
2. Lateral Length Calculation
Using Pythagorean theorem:
\[L = \sqrt{(R-r)^2 + h^2}\] \[L = \sqrt{(5-3)^2 + 4^2} = \sqrt{4 + 16}\] \[L = \sqrt{20} ≈ 4.47\]The lateral length is approximately 4.47 units
3. Volume Calculation
Using the three-term formula:
\[V = \frac{1}{3}\pi h(R^2 + Rr + r^2)\] \[V = \frac{1}{3}\pi \cdot 4 \cdot (25 + 15 + 9)\] \[V = \frac{1}{3}\pi \cdot 4 \cdot 49 = \frac{196\pi}{3} ≈ 205.11\]The volume is approximately 205.11 cubic units
4. Surface Area Calculation
Lateral + top + base:
\[S_L = \pi(R+r)L = \pi \cdot 8 \cdot 4.47 ≈ 112.33\] \[S = S_L + A_T + A_B\] \[S ≈ 112.33 + 28.27 + 78.54 = 219.14\]The total surface area is approximately 219.14 square units
5. The Perfect Truncated Cone
The truncated cone with perfect frustum geometry
Perimeter Calculations
Large Perimeter:
PL = 2πR = 2π × 5 = 10π ≈ 31.42
Small Perimeter:
PS = 2πr = 2π × 3 = 6π ≈ 18.85
The circumferences of both circular faces provide complete geometric characterization.
The Truncated Cone: Fundamental Frustum Geometry
The truncated cone (frustum) stands as one of the most fundamental and practically important geometric solids in mathematics and engineering. Created by cutting a cone with a plane parallel to its base, this elegant shape combines the simplicity of circular geometry with the sophistication of three-dimensional relationships. The truncated cone demonstrates perfect mathematical harmony through its volume formula, which elegantly incorporates three radius terms (R², Rr, r²), and its surface area calculations that seamlessly integrate circular and lateral geometries. From ancient architecture to modern industrial applications, the frustum continues to serve as a cornerstone of practical geometry and engineering design.
The Geometry of Parallel Sections
The truncated cone demonstrates the elegance of parallel sectioning:
- Cone section: Created by cutting a complete cone with a parallel plane
- Parallel faces: Two circular surfaces remain parallel after cutting
- Slanted sides: Lateral surface maintains conical characteristics
- Rotational symmetry: Perfect symmetry around the central axis
- Pythagorean relationships: Slant length follows right triangle principles
- Volume elegance: Three-term formula captures geometric essence
- Surface harmony: Sum of circular and lateral areas creates totality
Mathematical Elegance
Volume Formula Beauty
The volume formula V = (π/3)h(R² + Rr + r²) elegantly captures the frustum's geometric essence through three radius terms representing large, mixed, and small contributions.
Surface Area Integration
The total surface area seamlessly combines two circular areas with the lateral surface, demonstrating perfect geometric integration.
Practical Universality
From pipe reducers to architectural elements, the truncated cone provides optimal solutions for countless engineering and design challenges.
Mathematical Foundation
The frustum serves as a foundation for understanding more complex geometric relationships and advanced solid modeling techniques.
Summary
The truncated cone represents the perfect fusion of geometric elegance and practical utility, demonstrating how fundamental mathematical principles create forms of enduring importance. Its elegant three-term volume formula and harmonious surface area relationships showcase the mathematical beauty inherent in simple geometric operations. From ancient architectural applications to modern industrial design, the frustum continues to serve as a testament to the practical value of pure geometric relationships. As a bridge between basic circular geometry and advanced three-dimensional analysis, the truncated cone remains an essential element in the vocabulary of mathematics, engineering, and design. Its study reveals how the simple act of parallel sectioning can create forms of remarkable versatility and mathematical richness.