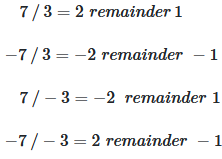Modulo
Description of Modulo, the remainder of a Euclidean division
Modulo is the remainder of a Euclidean division. As a standalone feature, modulo is included in most programming languages. It is treated there as a function or operator, usually with the abbreviation mod or %.
In mathematics, it corresponds to the remainder of a division, as described under division with remainder.
Example
In the example above is modulo = \(2\)
Dividing numbers with different signs also results in different signs for the results. In the following examples the mathematical division and the modulo function as they are integrated in computers are compared.
More information you can find under division with remainder
|
|