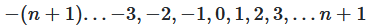Natural numbers
This page describes the natural and integer numbers
The natural numbers, also called positive integers, are the numbers
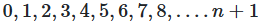 .
.
Natural numbers are infinitely, because every number n has a successor n + 1.
For natural numbers, there are two operations, addition and multiplication.
In addition, add two numbers \(a + b\) to a new number. Here, \(a\) and \(b\) are the summands and the result the sum.
In multiplication multiply two numbers \(a · b\) to a new number. \(a\) and \(b\) are called factors and the result is the product.
Integer numbers
Natural numbers can be added and multiplied without restriction. Substractions and divisions are limited. \(7 - 5 = 2\) or \(8 / 2 = 4\) can be calculated with natural numbers. With \(5 -7\) the range of natural numbers is left. The result \(-2\) falls within the range of the integer numbers
The integers expand the range of natural numbers by the negative range
The range of integers numbers is
|
|