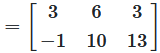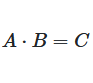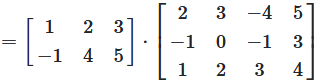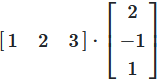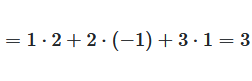Matrix Calculation

We can calculate with matrices, just as we do arithmetic with numbers. We can matrices calculate if we follow the rules for their arithmetic.

Because of this similarity, it is useful to distinguish between numbers and matrices in the way that we write symbols of numbers by lower case letters \((a, b, x, y)\) and matrices by upper case (capital) letters such as\((A, B, X, Y)\).

Matrices Scalar Multiplication

A matrix can multiply by a scalar (i.e., by an ordinary number) by multiplying each element in the matrix by that numbe

\(\displaystyle A=\begin{bmatrix}1 & -3 \\ 4 & 7 \end{bmatrix} · 2.5 =\begin{bmatrix}2.5 & -7.5 \\ 10 & 17.5 \end{bmatrix} \)

Addition and Subtraction of Matrices

For Matrices addition or subtraction, the matrices must conform. That is, they both must have the same number of rows and the same number of columns.

To execute the matrices addition, the corresponding matrices elements are added.

\(\displaystyle A=\begin{bmatrix}1 & 2 & -3\\ -4 & 5 & 6\end{bmatrix} + \begin{bmatrix}2 & 4 & 6 \\ 3 & 5 & 7\end{bmatrix} \)\(= \begin{bmatrix}3 & 6 & 3\\ -1 & 10 & 13\end{bmatrix} \)

Multiplying Matrices

There is a special rule for matrices multiplying, constructed in a way that is designed so that we can use it to represent simultaneous equations using matrices.

Multiplication of matrices is only allowed if the number of columns of the left matrix is the same as the number of rows of the right matrix.

The result is a matrix whose entries are given by the product sums of pairs in row vectors of the first and column vectors of the second matrix.

\(\displaystyle A·B=C=\begin{bmatrix}1 & 2 & 3 \\ -1 & 4 & 5\end{bmatrix} · \begin{bmatrix}2 & 3 & -4 & 5 \\ -1 & 0 & -1 & 3 \\ 1 & 2 & 3 & 4 \end{bmatrix} = \begin{bmatrix}3 & 9 & 3 & 23 \\ -1 & 7 & 15 & 27 \end{bmatrix} \)

The first element of the product \(C\), is the sum of the products of each element of the first row of \(A\), by the corresponding element of the first column of \(B\)

\(\displaystyle \begin{bmatrix}1 & 2 & 3 \end{bmatrix} · \begin{bmatrix}2 \\ -1 \\ 1 \end{bmatrix} = 1 · 2 + 2·(-1)+3·1=3\)