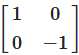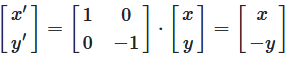Matrix reflection and shear
Description of reflection and shear of matrices with examples
Geometric operations, like rotating a position vector by a certain angle around some axis, can be achieved by multiplying the vector by an appropriate matrix. This page descript how such matrices are constructed.
Matrix Reflection
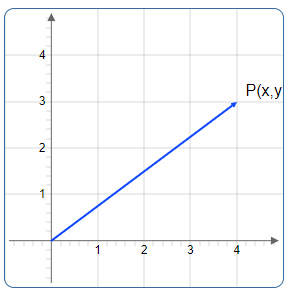
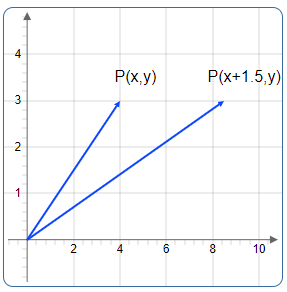
We will consider a point \(P\) with the coordinates \((x, y)\) in a two-dimensional space.
In the two dimensional space we draw the vector
 as
as
Matrices Calculation
Matrices Addition
Matrices Subtraction
Matrices Multiplication
Matrices Inverse Cramer method
Matrices Inverse Gauss-Jordan
Matrices and Simultaneous Equations
Matrices and Determinants
Row Operations of Matrices
Matrices and Geometry, Reflection
Matrices and Geometry, Plane Rotation
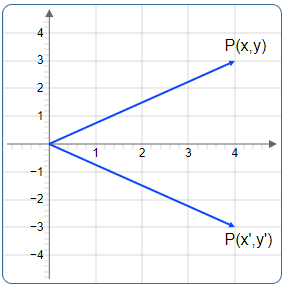
The matrix below produces a reflection of the vector across the X-axis
this results in the formula
A 3-dimensional reflection of the \(Y\) position is achieved by the following formula
To produce reflections in the \(X\) or \(Z\) planes, place a negative sign on the corresponding diagonal elements of the unit matrix.
Matrix Shear
The insertion of a non-zero element into a position outside the diagonal of the unit matrix produces a shear distortion of the position vector.
corresponds to
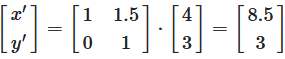
|
|