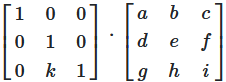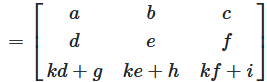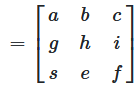Matrix and Row Operations

There are three types of elementary matrix row operations, corresponding to the operations that apply to equations to eliminate variable

• Adding a multiple of one row to another row

• Multiplying of a row by a non-zero scalar

• Interchange of two rows

These operations can be done manually, but also by matrices multiplication with a given matrix and some modified identity matrix. See the three examples below.

Adding a multiple of one row to another

• Placing \(k\) in the second column of row 3 of the identity matrix

• then multiplying the matrices.

• This has k-times the values of corresponding elements of row 2 added to those of row 3 of the matrix.

\(\displaystyle \left[\matrix{1&0&0\\0&1&0\\0&k&1}\right]˙ \left[\matrix{a&b&c\\d&e&f\\g&h&i}\right]= \left[\matrix{a&b&c\\d&e&f\\kd+g&ke+h&kf+i}\right]\)

The value of the determinant in the result is identical to the value of the source matrix \(A\)

Multiplying a row by a non-zero scalar:

\(\displaystyle \left[\matrix{1&0&0\\0&k&0\\0&0&1}\right] · \left[\matrix{a&b&cd\\d&e&f\\g&h&i}\right]= \left[\matrix{a&b&c\\kd&ke&kf\\g&h&i}\right]\)

The value of the determinant in the result is \(k\) times the value of the source matrix \(A\)

Interchanging two rows

\(\displaystyle \left[\matrix{1&0&0\\0&0&1\\0&1&0}\right]˙ \left[\matrix{a&b&c\\d&e&f\\g&h&i}\right]= \left[\matrix{a&b&c\\g&h&i\\s&e&f}\right]\)

The value of the determinant in the result is identical to the value of the source matrix \(A\)