Frustum Pyramide berechnen
Rechner und Formeln zur Berechnung einer Frustum Pyramide
Diese Funktion berechnet verschiedene Parameter einer Frustum Pyramide. Die Frustum Pyramide besteht aus einem regelmäßigen Frustum oder Pyramidenstumpf und einer auf die größere Basis aufgesetzten Pyramide.
Zur Berechnung geben Sie die Seitenlänge a und b, die Höhen der Pyramide und des Frustum (Pyramidenstumpf) und die Anzahl der Ecken ein. Dann klicken Sie auf den Button 'Rechnen'.
|
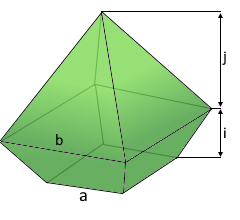
Formeln zur Frustum Pyramide
Gesamthöhe (\(\small{h}\))
\(\displaystyle h=i+j \)
Umfang der Basis (\(\small{P}\))
\(\displaystyle P =b\cdot n\)
Basisfläche (\(\small{A}\))
\(\displaystyle A = \frac{ n · a^2 }{ 4 · tan(\frac{π}{n})} \)
Mantelfläche Frustum (\(\small{L_F}\))
\(\displaystyle L_F = \frac{n}{4} \cdot (a + b) \cdot \sqrt{cot^2\left(\frac{π}{n}\right) \cdot (a - b)^2 + 4\cdot i^2 } \)
Mantelfläche Pyramide (\(\small{L_P}\))
\(\displaystyle L_P = n · b · \frac{\sqrt{j^2 + \frac{1}{4} · b^2 · cot^2(\frac{π}{n})}}{2} \)
Gesamte Oberfläche (\(\small{S}\))
\(\displaystyle S = A+ L_F+L_P \)
Volumen Frustum (\(\small{V_F}\))
\(\displaystyle V_F = \frac{i}{3} · \left(\frac{n · (a^2 + b^2)}{4 · tan(\frac{π}{n})} \displaystyle + \sqrt{\frac{ n^2 · a^2 · b^2 }{ (4 · tan(\frac{π}{n}))^2}} \right) \)
Volumen Pyramide (\(\small{V_P}\))
\(\displaystyle V_P = \frac{n · b^2 · j}{12 · tan(\frac{π}{n})} \)
Volumen (\(\small{V}\))
\(\displaystyle V = V_F+V_P \)

Dreieckige Pyramide • Quadratische Pyramide • Fünfeckige Pyramide • Sechseckige Pyramide • Siebeneckige Pyramide • Regelmäßige Pyramide • Quadratischer Pyramidenstumpf • Rechteckiger Pyramidenstumpf • Regelmäßiger Pyramidenstumpf • Dreieckige Doppelpyramide • Fünfeckige Doppelpyramide • Sechseckige Doppelpyramide • Doppelpyramide • Frustum Pyramide
|
|