Regelmäßiges Sechseckprisma berechnen
Rechner und Formel zur Berechnung eines regelmäßigen Sechseckprisma
Diese Funktion berechnet die Höhe oder das Volumen eines regelmäßigen Sechseckprisma.
Zur Berechnung geben Sie eine Seitenlänge der Basis und das Volumen oder die Höhe ein. Dann klicken Sie auf den Button 'Rechnen'.
|
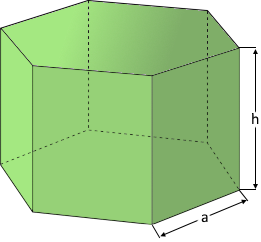
Formeln zum regelmäßigen Sechseckprisma
Oberfläche (\(\small{S}\))
\(\displaystyle S = 3 \cdot \sqrt{3} \cdot a^2 + 6 \cdot a \cdot h\)
Basisfläche (\(\small{A}\))
\(\displaystyle A = 1.5 \cdot \sqrt{3} \cdot a^2 \)
Höhe (\(\small{h}\))
\(\displaystyle h=\frac{2·V}{3 · \sqrt{3} · a^2}\)
Volumen (\(\small{V}\))
\(\displaystyle V=1.5 \cdot \sqrt{3} \cdot a^2 \cdot h\)
Quader
•
Quadratische Säule
•
Antiprisma
•
Sechseckprisma
•
Dreiecksprisma
•
Regelmäßiges Prisma
•
Schiefes Prisma
•
Rampe
•
Antiwürfel
•
Keil
•
Gerader Keil
•
Rhomboeder
•
Parallelepiped
•
Tetraeder, allgemeines
•
Pentagonales Trapezoeder
•
Tetragonales Trapezoeder
•
Prismatoid
•
Sterntetraeder
•
Dodekaederstern
•
Ikosaederstern
•
Großes Dodekaeder
Tetraeder • Würfel / Hexaeder • Oktaeder • Dodekaeder • Ikosaeder
Tetraeder • Würfel / Hexaeder • Oktaeder • Dodekaeder • Ikosaeder
|
|