Spheroid Calculator
Calculator and formulas for calculating volume and surface area of a spheroid
Spheroid Calculator
The Spheroid
The spheroid is a ellipsoid of revolution created by rotating an ellipse around one of its axes.
Spheroid Properties
The Spheroid: Created by ellipse rotation
Spheroid Types
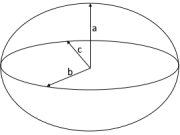
Oblate Spheroid
a < b - Lens shape like Earth
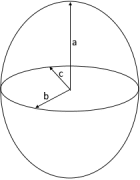
Prolate Spheroid
a > b - Rugby ball shape
Spheroids in nature.
From planets to molecules.
|
|
What is a spheroid?
The spheroid (ellipsoid of revolution) is a fundamental geometric shape:
- Definition: Created by rotating an ellipse around one of its axes
- Types: Oblate (flattened) and prolate (elongated)
- Properties: Rotationally symmetric around one axis
- Nature: Earth shape, planetary forms
- Technology: Containers, aerodynamic bodies
- Mathematics: Elegant formulas with π and square roots
Geometric properties of the spheroid
The spheroid shows fascinating geometric properties:
Basic parameters
- Semi-axes: a (rotation axis), b (equatorial)
- Meridian ellipse: Section through rotation axis
- Parallel circles: Circular cross-sections
- Rotational symmetry: Infinite mirror axes
Special properties
- Eccentricity: Measure of deviation from spherical form
- Flattening: f = (a-b)/a for oblate spheroids
- Curvature: Varies over the surface
- Geodesy: Foundation for Earth surveying
Mathematical relationships
The spheroid follows elegant mathematical laws:
Volume formula
Same formula for oblate and prolate forms. Elegant and simple.
Surface area formula
Different formulas for oblate/prolate. With arcsin/arcsinh functions.
Applications of the spheroid
Spheroids find applications in various fields:
Geodesy & Cartography
- Earth modeling (WGS84, GRS80)
- GPS coordinate systems
- Map projection
- Satellite orbits
Astronomy & Astrophysics
- Planetary shapes
- Asteroid modeling
- Stellar objects
- Gravitational fields
Engineering
- Container design
- Pressure tanks
- Aerodynamic bodies
- Optical lenses
Physics & Chemistry
- Atomic nuclei
- Molecular geometry
- Crystal structures
- Quantum mechanics
Formulas for the spheroid
Volume (V)
Universal formula for all spheroids
Surface Area (S) - Oblate
For flattened spheroids (a < b)
Surface Area (S) - Prolate
For elongated spheroids (a > b)
Sphere (Special case)
When a = b (perfect sphere)
Spheroid Parameters
\(e = \sqrt{1-\frac{b^2}{a^2}}\)
\(f = \frac{a-b}{a}\)
\(\frac{b}{a}\)
Oblate/Prolate
All parameters follow from the semi-axes a and b
Calculation example for a spheroid
Given
Find: Volume and surface area of the elongated spheroid
1. Volume calculation
For a = 6, b = 4:
\[V = \frac{4}{3} \cdot \pi \cdot 6 \cdot 4^2\] \[V = \frac{4}{3} \cdot \pi \cdot 6 \cdot 16\] \[V = \frac{4}{3} \cdot \pi \cdot 96 = 128\pi\] \[V ≈ 402.12 \text{ cm}^3\]The volume is approximately 402.12 cm³
2. Surface area calculation (Prolate)
Since a > b (6 > 4):
\[\sqrt{a^2-b^2} = \sqrt{36-16} = \sqrt{20} = 2\sqrt{5}\] \[\arcsin\left(\frac{2\sqrt{5}}{6}\right) ≈ 0.7297\] \[S = 2\pi \cdot 16 + \frac{2\pi \cdot 6 \cdot 16}{2\sqrt{5}} \cdot 0.7297\] \[S ≈ 271.77 \text{ cm}^2\]The surface area is approximately 271.77 cm²
3. Spheroid parameters
Additional parameters:
\[e = \sqrt{1-\frac{16}{36}} = \sqrt{\frac{5}{9}} ≈ 0.745\] \[f = \frac{6-4}{6} = \frac{1}{3} ≈ 0.333\] \[\frac{b}{a} = \frac{4}{6} = \frac{2}{3} ≈ 0.667\]Eccentricity, flattening and axis ratio
4. The elongated spheroid
The elongated spheroid (rugby ball shape)
The Spheroid: Perfection of nature and mathematics
The spheroid is a fascinating geometric shape that unites the elegance of nature and the precision of mathematics. Created by the rotation of an ellipse around one of its principal axes, it forms the foundation for describing the Earth's shape and countless other objects in nature and technology. The mathematical beauty lies in the elegant formulas with π, square roots and trigonometric functions that perfectly describe all geometric properties.
The geometry of rotation
The spheroid shows the perfection of rotationally symmetric geometry:
- Meridian ellipse: Every section through the rotation axis is an ellipse
- Parallel circles: All cross-sections are perfect circles
- Rotational symmetry: Infinite mirror planes through the axis
- Two basic types: Oblate (flattened) and prolate (elongated) forms
- Special case sphere: When both semi-axes are equal
- Geodetic significance: Foundation for Earth surveying
- Universal application: From atomic nuclei to galaxies
Mathematical elegance
Formula perfection
The volume formula is universally valid, while the surface area formulas for oblate and prolate forms show the beauty of integral and differential calculus.
Geodetic precision
As the foundation for GPS and cartography, the spheroid enables precise navigation and surveying on Earth.
Natural perfection
From Earth's shape to planetary forms to molecular structures - the spheroid is found everywhere in nature.
Technical perfection
In engineering and design, the spheroid offers optimal solutions for containers, aerodynamic bodies and optical systems.
Summary
The spheroid embodies the perfect harmony between mathematical elegance and practical application. Its shape, created by ellipse rotation and described by elegant formulas with π and square roots, makes it a fundamental building block of geometry. From the precise description of Earth's shape in geodesy through astronomical applications to engineering solutions - the spheroid connects theoretical beauty with practical utility. As a spheroid, it shows how the rotation of a simple ellipse leads to one of the most important geometric shapes in science and technology, shaping our world from the smallest molecular to the largest planetary scale.
|
|
|
|