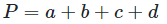Trapezoid

In geometry, a trapezoid is a flat square with two sides that are parallel to each other. The two parallel sides are called the base sides of the trapezoid. The longer base side is often referred to as the base of the trapezium, the two adjacent sides as the legs.

Properties

• It has two opposite sides, the bases, which are parallel to each other.
• The opposite sides are of different lengths.
• The height h of the trapezoid is the distance between the two parallel sides.
• The two angles adjacent to the legs complement each other to form 180 degrees.
• Every convex trapezoid has two diagonals that intersect each other in the same proportion.
• The middle segment \(m\) of a trapezoid is parallel to the bases. His measure is half the sum of the bases.

Formulas

Side lengths

Diagonal

Height

Medium width

Area

Perimeter

Angles

Trapezoid online calculator →