6dB Crossover
Calculation of a 1st order loudspeaker crossover with 6dB attenuation per octave
Crossover Calculator
6dB Crossover (1st Order)
The simplest crossover with only one component per way: An inductor for the woofer and a capacitor for the tweeter. Attenuation: 6dB per octave.
Frequency Response
Crossover attenuation in dB over frequency. Move your mouse over the chart for details.
Calculation Formulas
Inductor (Low-pass)
Capacitor (High-pass)
Variable Legend
| \(L\) | Inductor (Henry) |
| \(C\) | Capacitor (Farad) |
| \(Z\) | Impedance (Ohm) |
| \(f_C\) | Crossover frequency (Hz) |
| \(\pi\) | Pi ≈ 3.14159 |
Important Note
One of the speakers must be reverse-polarized because the membranes move in opposite directions due to phase shift.
Characteristics of 6dB Crossover (1st Order)
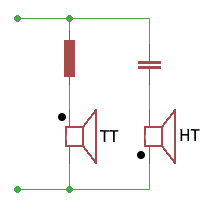
Circuit diagram of a 6dB crossover
Operation
The simplest crossover is the 1st order crossover with only one inductor for the bass speaker and one capacitor for the high-frequency range. A 1st order filter has good phase and transient response behavior.
Advantages
- Simple construction
- Few components
- Good phase behavior
- Cost-effective
Disadvantages
- Low attenuation (6dB/octave)
- Large overlap
- Tweeter is stressed
- Phase reversal necessary
Technical Details
Phase Behavior
Since in the inductor the current lags the voltage by 90° and in the capacitor the voltage also lags the current by 90°, the membranes of the speakers move in opposite directions.
Application Recommendation
To obtain clean reproduction, the transfer characteristics should still be linear within the overlap range for about 2 octaves.
Typical Application
6dB crossovers are used when a smooth transition between speakers is desired and the speakers cover a sufficiently broad frequency range.
Calculation Example
Given: 8Ω speaker, crossover frequency 2400Hz
\[L = \frac{8Ω}{2π × 2400Hz} ≈ 0.53\text{ mH}\]
\[C = \frac{1}{2π × 2400Hz × 8Ω} ≈ 8.3\text{ µF}\]
|
|