12dB Frequenzweiche
Berechnung einer Lautsprecher-Frequenzweiche 2. Ordnung mit 12dB Dämpfung pro Oktave
Frequenzweichen-Rechner
12dB Weiche (2. Ordnung)
Frequenzweiche mit zwei Bauteilen pro Weg: Je eine Spule und ein Kondensator für Tieftöner und Hochtöner. Dämpfung: 12dB pro Oktave (Butterworth-Charakteristik).
Schaltplan
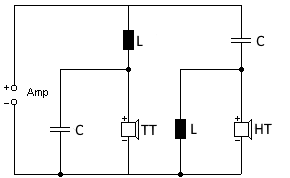
Schaltbild einer 12dB Frequenzweiche (2. Ordnung)
Die berechneten Werte werden automatisch in den Schaltplan eingetragen. Beide Wege verwenden identische Bauteilwerte.
Berechnungsformeln
Spule (Butterworth 2. Ordnung)
Kondensator (Butterworth 2. Ordnung)
Variablen-Legende
| \(L\) | Spule (Henry) |
| \(C\) | Kondensator (Farad) |
| \(Z\) | Impedanz (Ohm) |
| \(f_C\) | Crossover-Frequenz (Hz) |
| \(\sqrt{2}\) | Butterworth-Faktor ≈ 1,414 |
Phasenverhalten
Bei 12dB Weichen bewegen sich beide Lautsprecher in Phase. Keine Umpolung erforderlich!
Eigenschaften der 12dB Weiche (2. Ordnung)
Funktionsweise
Eine Frequenzweiche 2. Ordnung benötigt 2 Bauteile in jedem Zweig und bietet eine Flankensteilheit von 12dB pro Oktave. Die Werte der Kondensatoren und Spulen im Hoch- und Tiefpass sind identisch. Diese Weiche basiert auf der Butterworth-Charakteristik mit einem Q-Faktor von 0,707.
Vorteile
- Bessere Trennung (12dB/Oktave)
- Standard für HiFi-Anwendungen
- Keine Umpolung erforderlich
- Flacher Frequenzgang
Nachteile
- Mehr Bauteile erforderlich
- Höhere Kosten
- Komplexere Schaltung
- Höhere Verluste
Technische Details
Phasenverhalten
Da im Tiefpass bei der Übernahmefrequenz der Strom gegenüber der Spannung um 180° nacheilt und am Hochpass die Spannung gegenüber dem Strom ebenfalls um 180° nacheilt, bewegen sich die Membranen der Lautsprecher in Phase.
Butterworth-Charakteristik
Die 12dB Weiche verwendet die Butterworth-Charakteristik mit einem Q-Faktor von 0,707. Dies ergibt einen maximally flat response im Durchlassbereich.
Typische Anwendung
12dB Weichen sind der Standard für hochwertige HiFi-Lautsprecher. Sie bieten eine gute Balance zwischen Trennschärfe und Phasenverhalten.
Berechnungsbeispiel
Gegeben: 8Ω Lautsprecher, Trennfrequenz 2400Hz
\[L = \frac{\sqrt{2} \cdot 8Ω}{2π \times 2400Hz} ≈ 0,75\text{ mH}\]
\[C = \frac{\sqrt{2}}{4π \times 2400Hz \times 8Ω} ≈ 5,9\text{ µF}\]
Vergleich der Weichen-Ordnungen
| Ordnung | Dämpfung | Bauteile pro Weg | Phasenverhalten | Anwendung |
|---|---|---|---|---|
| 1. Ordnung | 6dB/Oktave | 1 (L oder C) | Umpolung nötig | Einfache Systeme |
| 2. Ordnung | 12dB/Oktave | 2 (L und C) | Keine Umpolung | HiFi-Standard |
| 3. Ordnung | 18dB/Oktave | 3 (L-C-L oder C-L-C) | Umpolung nötig | Professionell |