R/C for given charging voltage
Calculation of R or C for a given charging voltage at a specific time
Calculate R/C for charging voltage
RC Charging Process
On this page you can calculate the values of a capacitor or resistor that are required to achieve a specific charging voltage on a capacitor at a given time.
RC Charging Process
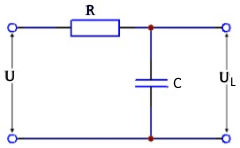
Legend
Calculation formulas
Charging Process
- Exponential function: UC(t) = U(1 - e-t/τ)
- Time constant: τ = RC
- 63% after τ: After one time constant
- 99% after 5τ: Practically fully charged
RC Charging Process - Theory and Applications
The Capacitor Charging Process
When charging a capacitor through a resistor, the voltage across the capacitor follows an exponential function. The charging speed is determined by the time constant τ = RC. These calculations make it possible to determine the required component values for a desired charging voltage at a specific time.
Mathematical Foundations
Charging voltage over time
Exponential function of the charging process with Ω = RC
Rearrangement for R and C
Normalized form for component calculation
Time Constant and Charging Behavior
After 1τ (63%)
After one time constant the capacitor is 63% charged.
After 3τ (95%)
After three time constants practically fully charged.
After 5τ (99%)
After five time constants full charge is reached.
Practical Applications
Timing Circuits:
Power Supply:
Signal Processing:
Calculation Examples
Example 1: Calculate resistor
Given: C = 10µF, U = 12V, UC = 8V, t = 10ms
Result: The required resistor is approximately 918Ω.
Example 2: Calculate capacitor
Given: R = 1kΩ, U = 5V, UC = 3V, t = 1ms
Result: The required capacitance is approximately 1.1µF.
Design Considerations
Important Design Aspects
- Time constant: τ = RC determines the charging speed
- Voltage rating: Capacitor must be rated for operating voltage
- Leakage current: Real capacitors have parasitic resistances
- Tolerances: Component variations affect timing behavior
- Temperature influence: Capacitance and resistance are temperature dependent
- ESR: Equivalent series resistance affects behavior
Discharge Process
Capacitor Discharge
During discharge, the voltage follows a falling exponential function. After one time constant, 37% of the initial voltage remains.