Calculate RC Differentiator
Calculator and formulas for calculating an RC differentiator circuit
Calculate Differentiator
RC Differentiator Circuit
This function can calculate the properties of an RC differentiator circuit. The function calculates the capacitor, resistor, or period/frequency.
Differentiator Circuit
Pulse Shaping Stage
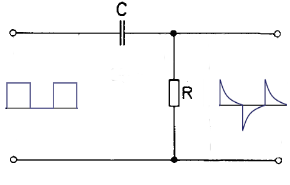
The differentiator functions as a pulse shaping stage. The CR circuit generates a pulse-like AC voltage at the output from a square wave voltage at the input.
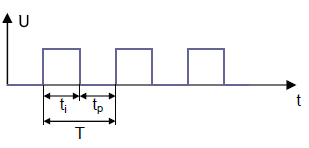
Time Constant τ (tau)
The time constant of an RC circuit is the product of R · C. The unit is seconds. The symbol is the Greek letter τ (tau).
After 5τ, the charge is approximately 99.3%.
|
|
RC Differentiator - Theory and Formulas
How the Differentiator Works
The differentiator functions as a pulse shaping stage. The CR circuit generates a pulse-like AC voltage at the output from a square wave voltage at the input.
Pulse Shapes with Different Time Constants
t1 = 5τ Optimal Differentiation
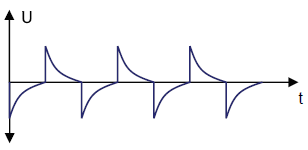
When the length of the square wave pulse (t1) equals 5 times the time constant τ, an optimal pulse sequence is created.
t1 = 10τ Short Pulses
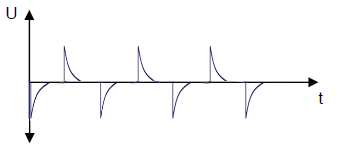
When the pulse duration is much greater than 5τ, short pulses equal to the input voltage amplitude are generated.
Time Constant and Charging Behavior
The Time Constant τ (tau)
- The time constant is the product of R × C
- Unit: Seconds (s)
- Symbol: τ (Greek letter tau)
- After 5τ, the charge is approximately 99.3%
- Determines the speed of charge/discharge processes
Practical Applications
Signal Processing:
Digital Technology:
Measurement Technology:
Design Guidelines
Optimal Dimensioning
- For clean differentiation: t1 ≥ 5τ
- For short pulses: t1 ≥ 10τ
- Output amplitude: Approximately equal to input amplitude
- Pulse width: Dependent on time constant
- Loading: High input impedance of following amplifier
- Frequency range: Dependent on τ and desired pulse shape
Mathematical Relationships
Basic Formulas
Where n is the factor (typically 5 or 10)
Conversions
Calculation of components for given t1