RMS value of a sawtooth pulse

Calculator and formulas for calculating the RMS value of a sawtooth pulse voltage

Sawtooth Pulse Calculator

Sawtooth pulse voltage

Enter the values for pulse duration (t_i), period duration (T), and the peak voltage U_s of the pulse.

Pulse duration t_i

Period duration T

Pulse voltage U_s

Decimal places

Results

RMS voltage:

Mean voltage:

Sawtooth pulse & parameters

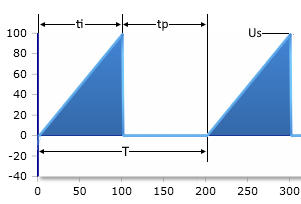
Parameters

\(\displaystyle U_s\) = Peak voltage [V]

\(\displaystyle U_{eff}\) = RMS voltage [V]

\(\displaystyle U_m\) = Mean voltage [V]

\(\displaystyle T\) = Period duration [ms]

\(\displaystyle t_i\) = Pulse duration [ms]

Basic formulas

\[U_{eff} = \sqrt{\frac{t_i}{T \cdot 3}} \cdot U_s\]

\[U_m = \frac{U_s \cdot t_i}{2 \cdot T}\]

Example calculations

Practical calculation examples

Example 1: 50% duty cycle

Given: U_s = 10V, t_i = 50ms, T = 100ms

\[U_{eff} = \sqrt{\frac{50}{100 \cdot 3}} \cdot 10V = \sqrt{\frac{1}{6}} \cdot 10V = 4{,}08V\]

\[U_m = \frac{10V \cdot 50ms}{2 \cdot 100ms} = \frac{500}{200} = 2{,}5V\]

Typical sawtooth signal with 50% duty cycle

Example 2: 25% duty cycle

Given: U_s = 12V, t_i = 25ms, T = 100ms

\[U_{eff} = \sqrt{\frac{25}{100 \cdot 3}} \cdot 12V = \sqrt{\frac{1}{12}} \cdot 12V = 3{,}46V\]

\[U_m = \frac{12V \cdot 25ms}{2 \cdot 100ms} = \frac{300}{200} = 1{,}5V\]

Low duty cycle for energy saving

Example 3: Oscilloscope application

Given: U_s = 5V, t_i = 2ms, T = 10ms (20% duty cycle)

\[U_{eff} = \sqrt{\frac{2}{10 \cdot 3}} \cdot 5V = \sqrt{\frac{1}{15}} \cdot 5V = 1{,}29V\]

\[U_m = \frac{5V \cdot 2ms}{2 \cdot 10ms} = \frac{10}{20} = 0{,}5V\]

Typical for time base generators

Duty cycle effects for sawtooth

RMS factor:

Formula: √(t_i/(T·3))

At 50%: √(1/6) ≈ 0.408

At 25%: √(1/12) ≈ 0.289

At 10%: √(1/30) ≈ 0.183

Mean value factor:

Formula: t_i/(2·T)

At 50%: 0.25

At 25%: 0.125

At 10%: 0.05

Formulas for sawtooth pulse

What is a sawtooth pulse?

The RMS value (Root Mean Square) of a sawtooth pulse can be calculated using the general formula for the RMS value of a periodic signal. It is defined as the DC value with the same thermal effect as the considered AC value. For sawtooth pulse voltages, it is calculated as follows.

Definition of RMS value

In a sawtooth pulse, the voltage rises linearly from 0V to the peak value U_s over the pulse duration t_i, and then remains at 0V for the rest of the period. The entered parameters for T and t_i must have the same unit.

RMS value

\[U_{eff} = \sqrt{\frac{t_i}{T \cdot 3}} \cdot U_s\]

Depends on the duty cycle and factor 1/√3.

Mean value

\[U_m = \frac{U_s \cdot t_i}{2 \cdot T}\]

Half the value of the rectangular pulse.

Mathematical derivation

Calculation

For a sawtooth pulse over a period T:

\[U_{eff} = \sqrt{\frac{1}{T} \int_0^T u^2(t) \, dt}\]

For 0 ≤ t ≤ t_i: u(t) = U_s · t/t_i (linearly rising)

For t_i < t ≤ T: u(t) = 0

\[U_{eff} = \sqrt{\frac{1}{T} \int_0^{t_i} \left(\frac{U_s \cdot t}{t_i}\right)^2 dt} = U_s \sqrt{\frac{t_i}{3T}}\]

Practical applications

Measurement technology

Oscilloscope time base
Sweep generators
Voltage ramps
ADC test patterns

Signal processing

Frequency modulation
VCO control
Wobbler signals
Linearization

Control engineering

Ramp generator
Setpoint specification
Integrator test
Time control

Comparison with other signal forms

RMS factors at 50% duty cycle

Rectangular pulse:
U_eff = U_s/√2 ≈ 0.707

Triangular pulse:
U_eff = U_s/√3 ≈ 0.577

Sawtooth pulse:
U_eff = U_s/√6 ≈ 0.408

Sine pulse:
U_eff = U_s/2 = 0.5

Spectral properties

Harmonics in sawtooth pulses

Sawtooth pulses contain all harmonics with a specific distribution:

DC component: U_s · D/2 (D = duty cycle)

Fundamental: Amplitude proportional to sin(πD)/(πD)

Harmonics: Amplitude ∝ sin(nπD)/(nπD)²

Special feature: Harmonics decrease as 1/n² (faster than square wave)

Design notes

Practical considerations

Linearity: Constant rise rate important for precision
Bandwidth: Fast rising edge requires high bandwidth
Offset errors: Can affect linearity
Temperature stability: Important for precise ramp generators
Reset: Fast reset to 0V required
Load: Capacitive loads can degrade linearity

Is this page helpful?

Thank you for your feedback!

Sorry about that
How can we improve it?

AC functions