RMS value of a rectangular pulse voltage
Calculator and formulas for calculating the RMS value of a rectangular pulse voltage
Rectangular Pulse Calculator
Rectangular Pulse Voltage
Enter the values for pulse duration (ti), period duration (T), and the peak voltage Us of the pulse.
Rectangular pulse & parameters
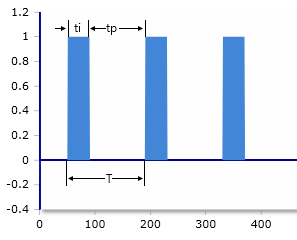
Parameters
Basic formulas
Example calculations
Practical calculation examples
Example 1: 50% duty cycle
Given: Us = 10V, ti = 50ms, T = 100ms
Example 2: 20% duty cycle
Given: Us = 10V, ti = 20ms, T = 100ms
Example 3: PWM signal
Given: Us = 5V, ti = 3ms, T = 10ms (30% PWM)
Duty cycle effects
RMS ratio:
Mean value ratio:
Formulas for rectangular pulse
What is a rectangular pulse voltage?
The RMS value of a rectangular pulse voltage depends on how the voltage changes over time. A rectangular pulse voltage usually has a fixed peak value Us and alternates between two voltage values over time, for example Us and 0 V or Us and -Us.
The calculator above computes the variant with Us and 0 V. The pulse length can vary.
Definition of RMS value
The RMS value is defined as the DC value with the same thermal effect as the considered AC value. Suppose the voltage has a positive value Us for part of the time and is 0V for the rest of the time, then the RMS value of the rectangular pulse voltage is calculated as:
RMS value
Depends on the duty cycle ti/T.
Mean value
Proportional to the duty cycle.
Mathematical derivation
Calculation
For a rectangular pulse over a period T:
Practical applications
Digital technology
- Clock signals
- PWM control
- Logic levels
- Trigger signals
Power electronics
- Switching regulators
- Motor control
- LED dimmers
- DC-DC converters
Measurement technology
- Oscilloscopes
- Signal generators
- Pulse width analysis
- Duty cycle measurement
Duty cycle and properties
Duty cycle
The duty cycle D defines the ratio of pulse duration to period duration:
Ueff = 0.316 · Us
Um = 0.1 · Us
Ueff = 0.5 · Us
Um = 0.25 · Us
Ueff = 0.707 · Us
Um = 0.5 · Us
Ueff = 0.949 · Us
Um = 0.9 · Us
Spectral properties
Harmonics in rectangular pulses
Rectangular pulses contain all harmonics with decreasing amplitude:
Design notes
Practical considerations
- Power dissipation: P = Ueff²/R - important for dimensioning
- EMC: Rectangular pulses generate broadband interference
- Filtering: Lower duty cycles require stronger filters
- Switching times: Real pulses have finite rise/fall times
- Measurement technology: Instrument bandwidth must be sufficient
- Cooling: High duty cycles increase thermal load
|
|