Calculate Angle Between Two Lines
Online calculator for calculating the intersection angle of two lines in the coordinate system
Line Angle Calculator
Intersection Angle of Two Lines
Calculates the angle α between two lines in the coordinate system through vector calculation or slope comparison.
Visualization
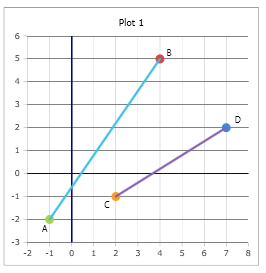
The graphic shows two intersecting lines with the calculated intersection angle.
The smaller of the two angles is output as the result (0° to 90°).
What is the Angle Between Two Lines?
The intersection angle between two lines is the smaller of the two angles that are created when they intersect:
- Acute angle: Always between 0° and 90°
- Unique: The smaller of the four resulting angles
- Symmetry: Order of lines doesn't matter
- Parallel lines: Angle = 0°
- Perpendicular lines: Angle = 90°
- Calculation: Via vectors or slopes
Calculation via Vector Analysis
The exact calculation is done using the direction vectors of the two lines:
Direction Vectors
Direction vectors of both lines
Angle Formula
Cosine of the intersection angle
Alternative Calculation via Slopes
The angle can also be calculated using the slopes of the two lines:
Calculate slopes
Slopes of both lines
Angle from slopes
Difference of slope angles
Formulas for Intersection Angle
Main Formula - Angle via Vectors
Angle between direction vectors (always acute angle through absolute value)
Calculate dot product
Dot product of direction vectors
Calculate vector magnitudes
Length of direction vectors
Slope formula
Angle via slope difference
Special cases
Perpendicular lines
Example
Example Calculation
Direction vectors
Differences of coordinates
Dot product
Calculate dot product
Magnitudes
Calculate vector lengths
Result
The intersection angle is approximately 23.46°
Understanding Intersection Angles of Two Lines
The intersection angle between two lines is an important concept in analytical geometry. It describes the smaller of the two angles that are created when two lines intersect at a point. This angle always lies between 0° and 90°.
Mathematical Foundations
There are various methods for calculating the intersection angle:
1. Vector Analysis (preferred method)
The most exact method uses the direction vectors of the two lines. For line 1 through A(x₁,y₁) and B(x₂,y₂) and line 2 through C(x₃,y₃) and D(x₄,y₄), the direction vectors are:
The angle then results from the dot product:
2. Slope Calculation
Alternatively, the angle can be calculated using the slopes m₁ and m₂ of the two lines:
Important Properties
Acute Angle
The intersection angle is always the smaller of the four resulting angles, i.e., between 0° and 90°.
Symmetry
The order of lines doesn't matter. The angle between line 1 and 2 equals the angle between 2 and 1.
Uniqueness
For each pair of lines, there is exactly one intersection angle (except for parallel lines).
Complementary Angles
The two intersection angles add up to 180°. We use the smaller one.
Special Cases
Parallel Lines
Angle = 0°
Same slope: m₁ = m₂
Perpendicular Lines
Angle = 90°
Slopes: m₁ · m₂ = -1
45° Angle
Occurs when one slope is the negative reciprocal of the other
Practical Applications
The calculation of intersection angles is found in many areas:
- Architecture: Roof slopes, building angles, construction drawings
- Mechanical engineering: Joint angles, cutting angles of components
- Surveying: Angles between survey lines, boundary courses
- Navigation: Course angles, bearing angles
- Computer graphics: Collision detection, 3D rendering
- Optics: Reflection and refraction angles
Mathematical Background
The dot product used for angle calculation is a fundamental concept of linear algebra. It measures both the "similarity" of directions and the lengths of the vectors. The cosine of the angle corresponds to the dot product normalized to the lengths.
Using the absolute value in the dot product ensures that the acute angle is always calculated, regardless of the orientation of the direction vectors.
|
|