Winkel zwischen zwei Geraden berechnen
Online Rechner zum Berechnen des Schnittwinkels zweier Geraden im Koordinatensystem
Geradenwinkel Rechner
Schnittwinkel zweier Geraden
Berechnet den Winkel α zwischen zwei Geraden im Koordinatensystem durch Vektorrechnung oder Steigungsvergleich.
Visualisierung
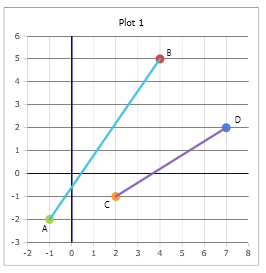
Die Grafik zeigt zwei sich schneidende Geraden mit dem berechneten Schnittwinkel.
Der kleinere der beiden Winkel wird als Ergebnis ausgegeben (0° bis 90°).
Was ist der Winkel zwischen zwei Geraden?
Der Schnittwinkel zwischen zwei Geraden ist der kleinere der beiden Winkel, die beim Schneiden entstehen:
- Spitzer Winkel: Immer zwischen 0° und 90°
- Eindeutig: Der kleinere der vier entstehenden Winkel
- Symmetrie: Reihenfolge der Geraden ist egal
- Parallele Geraden: Winkel = 0°
- Senkrechte Geraden: Winkel = 90°
- Berechnung: Über Vektoren oder Steigungen
Berechnung über Vektorrechnung
Die exakte Berechnung erfolgt über die Richtungsvektoren der beiden Geraden:
Richtungsvektoren
Richtungsvektoren beider Geraden
Winkelformel
Kosinus des Schnittwinkels
Alternative Berechnung über Steigungen
Der Winkel kann auch über die Steigungen der beiden Geraden berechnet werden:
Steigungen berechnen
Steigungen beider Geraden
Winkel aus Steigungen
Differenz der Steigungswinkel
Formeln für den Schnittwinkel
Hauptformel - Winkel über Vektoren
Winkel zwischen Richtungsvektoren (immer spitzer Winkel durch Betrag)
Skalarprodukt berechnen
Skalarprodukt der Richtungsvektoren
Vektorbeträge berechnen
Länge der Richtungsvektoren
Steigungsformel
Winkel über Steigungsdifferenz
Spezialfälle
Senkrechte Geraden
Beispiel
Beispielrechnung
Richtungsvektoren
Differenzen der Koordinaten
Skalarprodukt
Skalarprodukt berechnen
Beträge
Vektorlängen berechnen
Ergebnis
Der Schnittwinkel beträgt etwa 23.46°
Schnittwinkel zweier Geraden verstehen
Der Schnittwinkel zwischen zwei Geraden ist ein wichtiges Konzept der analytischen Geometrie. Er beschreibt den kleineren der beiden Winkel, die entstehen, wenn sich zwei Geraden in einem Punkt schneiden. Dieser Winkel liegt immer zwischen 0° und 90°.
Mathematische Grundlagen
Es gibt verschiedene Methoden zur Berechnung des Schnittwinkels:
1. Vektorrechnung (bevorzugte Methode)
Die exakteste Methode verwendet die Richtungsvektoren der beiden Geraden. Für Gerade 1 durch A(x₁,y₁) und B(x₂,y₂) sowie Gerade 2 durch C(x₃,y₃) und D(x₄,y₄) sind die Richtungsvektoren:
Der Winkel ergibt sich dann aus dem Skalarprodukt:
2. Steigungsberechnung
Alternativ kann der Winkel über die Steigungen m₁ und m₂ der beiden Geraden berechnet werden:
Wichtige Eigenschaften
Spitzer Winkel
Der Schnittwinkel ist immer der kleinere der vier entstehenden Winkel, also zwischen 0° und 90°.
Symmetrie
Die Reihenfolge der Geraden spielt keine Rolle. Der Winkel zwischen Gerade 1 und 2 ist gleich dem zwischen 2 und 1.
Eindeutigkeit
Für jedes Geradenpaar gibt es genau einen Schnittwinkel (außer bei parallelen Geraden).
Komplementärwinkel
Die beiden Schnittwinkel ergänzen sich zu 180°. Wir verwenden den kleineren.
Spezialfälle
Parallele Geraden
Winkel = 0°
Gleiche Steigung: m₁ = m₂
Senkrechte Geraden
Winkel = 90°
Steigungen: m₁ · m₂ = -1
45°-Winkel
Tritt auf, wenn eine Steigung das Negative der Kehrwerts der anderen ist
Praktische Anwendungen
Die Berechnung von Schnittwinkeln findet sich in vielen Bereichen:
- Architektur: Dachneigungen, Gebäudewinkel, Konstruktionszeichnungen
- Maschinenbau: Fügewinkel, Schnittwinkel von Bauteilen
- Vermessung: Winkel zwischen Vermessungslinien, Grenzverläufen
- Navigation: Kurswinkel, Peilungswinkel
- Computergrafik: Kollisionserkennung, 3D-Rendering
- Optik: Reflexions- und Brechungswinkel
Mathematischer Hintergrund
Das Skalarprodukt, das für die Winkelberechnung verwendet wird, ist ein fundamentales Konzept der linearen Algebra. Es misst sowohl die "Ähnlichkeit" der Richtungen als auch die Längen der Vektoren. Der Kosinus des Winkels entspricht dem auf die Längen normierten Skalarprodukt.
Die Verwendung des Betrags im Skalarprodukt stellt sicher, dass immer der spitze Winkel berechnet wird, unabhängig von der Orientierung der Richtungsvektoren.
|
|