Entfernung zwischen zwei Punkten berechnen
Online Rechner zum Berechnen der Distanz zwischen zwei Punkten im Koordinatensystem
Distanz Rechner
Koordinaten-Distanz
Berechnet die Entfernung zwischen zwei Punkten A(x₁,y₁) und B(x₂,y₂) mittels Pythagoräischem Lehrsatz.
Visualisierung
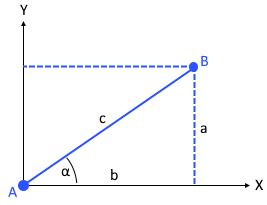
Die Grafik zeigt die geometrische Beziehung zwischen den beiden Punkten A und B.
Das entstehende rechtwinklige Dreieck ermöglicht die Anwendung des Satzes von Pythagoras.
Wie funktioniert die Distanzberechnung?
Die Entfernung zwischen zwei Punkten wird mit der Distanzformel berechnet:
- Eingabe: Koordinaten der Punkte A(x₁,y₁) und B(x₂,y₂)
- Berechnung: Anwendung des Satzes von Pythagoras
- Ergebnis: Direkte Entfernung zwischen den Punkten
- Zusätzlich: Einzelne X- und Y-Distanzen
- Winkel: Neigungswinkel zur X-Achse
- Reihenfolge: Punkt A und B sind austauschbar
Der Satz des Pythagoras in der Koordinatengeometrie
Die Distanzformel basiert auf dem Satz des Pythagoras:
Rechtwinkliges Dreieck
Grundformel des Pythagoras
Distanzformel
Angewendet auf Koordinaten
Formeln und Berechnungen
Hauptformel - Distanz zwischen zwei Punkten
Die fundamentale Distanzformel in der Koordinatengeometrie
Einzelne Koordinaten-Distanzen
Abstände in X- und Y-Richtung (Katheten des Dreiecks)
Winkelberechnung
Neigungs Winkel der Verbindungslinie zur X-Achse
Alternative Winkelformeln
Winkelberechnung über Sinus und Kosinus
Beispiel
Beispielrechnung
Berechnung
Die Distanz beträgt 10 Einheiten
Einzeldistanzen
- X-Distanz: |8-0| = 8
- Y-Distanz: |6-0| = 6
- Winkel α: arctan(6/8) ≈ 36.87°
Anwendungen
Navigation, Kartografie, Computergrafik, Robotik, GPS-Systeme.
Konstruktion der Entfernungsformel
Die Entfernungsformel zwischen zwei Punkten basiert auf dem berühmten Satz des Pythagoras. Wenn wir zwei Punkte A(x₁,y₁) und B(x₂,y₂) in einem Koordinatensystem haben, bilden diese zusammen mit einem dritten Punkt ein rechtwinkliges Dreieck.
Geometrische Herleitung
In der obigen Grafik bilden die beiden Strecken a und b die Katheten eines rechtwinkligen Dreiecks. Die Strecke c ist die Hypotenuse und entspricht der gesuchten Distanz zwischen den Punkten A und B.
Koordinaten-Transformation
Die Werte für die Katheten a und b ergeben sich aus den Differenzen der entsprechenden Koordinaten:
- Kathete a (Y-Richtung): a = |y₂ - y₁|
- Kathete b (X-Richtung): b = |x₂ - x₁|
Da wir die Werte quadrieren, können wir die Betragsstriche weglassen, da (±n)² = n² ist. Dies führt zur finalen Distanzformel:
|
|