Koch Kurve berechnen
Online Rechner und Formeln zur Berechnung der Koch Kurve - Fraktale Schneeflocke
Koch Kurve Rechner
Fraktale Koch Kurve
Berechnet die fraktalen Eigenschaften der Koch Kurve nach n Iterationen - auch bekannt als Kochsche Schneeflocke.
Visualisierung
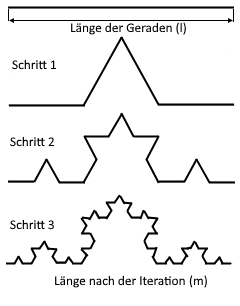
Die Grafik zeigt die iterative Konstruktion der Koch Kurve durch Dreiteilung und Dreiecksaufbau.
Jede Iteration erhöht die Komplexität und Länge der fraktalen Kurve.
Was ist die Koch Kurve?
Die Koch Kurve ist eine der berühmtesten fraktalen Kurven der Mathematik:
- Fraktal: Selbstähnliche, unendlich detaillierte Struktur
- Stetig: Überall zusammenhängend, aber nirgends differenzierbar
- Schneeflocke: Drei Koch Kurven bilden die Kochsche Schneeflocke
- Iterativ: Entsteht durch wiederholte Anwendung einer Regel
- Unendliche Länge: Begrenzte Fläche, aber unendliche Randlänge
- Dimension: Fraktale Dimension zwischen 1 und 2
Konstruktion der Koch Kurve
Die Koch Kurve entsteht durch iterative Anwendung einer einfachen Konstruktionsregel:
Schritt 1: Dreiteilung
Jede Strecke wird in drei gleiche Teile geteilt. Das mittlere Drittel wird entfernt.
Schritt 2: Dreieck aufbauen
Über die Lücke wird ein gleichseitiges Dreieck errichtet, dessen Basis entfernt wird.
Fraktale Eigenschaften
Die Koch Kurve zeigt typische fraktale Eigenschaften:
Selbstähnlichkeit
Jeder Teil sieht aus wie das Ganze, nur kleiner
Unendliche Länge
Die Länge wächst mit jeder Iteration um Faktor 4/3
Iterationsprozess verstehen
Bei jeder Iteration entstehen neue Details und die Eigenschaften ändern sich:
n = 0
Gerade Linie
Länge: l
4 × 1 = 1 Segment
n = 1
Erstes Dreieck
Länge: 4l/3
4 × 1 = 4 Segmente
n = 2
Vier Dreiecke
Länge: 16l/9
4 × 4 = 16 Segmente
Koch Kurve Formeln
Länge nach n Iterationen
Die Länge wächst exponentiell mit jeder Iteration
Höhe der Koch Kurve
Höhe des ersten Dreiecks
Umkehrformel für Länge
Ursprungslänge aus Iterationslänge
Länge aus Höhe
Ursprungslänge aus gegebener Höhe
Fraktale Dimension
Hausdorff-Dimension der Koch Kurve
Symbole und Bezeichnungen
- l: Länge der ursprünglichen Geraden
- h: Höhe des ersten Dreiecks
- m: Länge nach n Iterationen
- n: Anzahl der Iterationen
- D: Fraktale Dimension
- 4/3: Längen-Wachstumsfaktor
Beispiel
Beispielrechnung
1. Höhe berechnen
Höhe des ersten Dreiecks
2. Länge nach 3 Iterationen
Mehr als doppelte Länge!
3. Segmente zählen
Exponentielles Wachstum der Komplexität
Eigenschaften
- Selbstähnlich: Jeder Teil ist eine Miniatur des Ganzen
- Unendlich: Tendiert zu unendlicher Länge
- Fraktal: Dimension ≈ 1.26
Die Koch Kurve - Fraktale Geometrie verstehen
Die Koch Kurve, benannt nach dem schwedischen Mathematiker Helge von Koch (1904), ist eine der bekanntesten fraktalen Kurven und ein Paradebeispiel für die faszinierenden Eigenschaften der fraktalen Geometrie. Sie ist überall stetig, aber nirgends differenzierbar und besitzt eine fraktale Dimension zwischen 1 und 2.
Historischer Hintergrund
Die Koch Kurve wurde 1904 von Helge von Koch als Beispiel für eine stetige, aber nicht differenzierbare Kurve eingeführt. Sie war eines der ersten formal beschriebenen fraktalen Objekte, lange bevor der Begriff "Fraktal" von Benoit Mandelbrot geprägt wurde.
Konstruktionsprinzip
Die Konstruktion der Koch Kurve folgt einem einfachen, aber mächtigen Prinzip:
- Ausgangslinie: Man beginnt mit einer geraden Linie der Länge l
- Dreiteilung: Die Linie wird in drei gleiche Teile geteilt
- Entfernung: Das mittlere Drittel wird entfernt
- Dreieck: Über die entstandene Lücke wird ein gleichseitiges Dreieck errichtet
- Iteration: Dieser Prozess wird auf jeden neuen Linienabschnitt angewendet
Mathematische Eigenschaften
Exponentielles Längenwachstum
Die Länge wächst mit jeder Iteration um den Faktor 4/3, was zu unendlicher Länge führt.
Fraktale Dimension
Die Hausdorff-Dimension beträgt log(4)/log(3) ≈ 1.26, zwischen Linie und Fläche.
Selbstähnlichkeit
Jeder Teil der Kurve ist eine verkleinerte Kopie des Ganzen - perfekte Selbstähnlichkeit.
Nicht-Differenzierbarkeit
An keinem Punkt existiert eine eindeutige Tangente - die Kurve hat überall "Ecken".
Die Kochsche Schneeflocke
Wenn drei Koch Kurven zu einem geschlossenen Dreieck zusammengefügt werden, entsteht die berühmte Kochsche Schneeflocke. Diese besitzt die paradoxe Eigenschaft, eine endliche Fläche bei unendlichem Umfang zu haben.
Anwendungen und Bedeutung
Die Koch Kurve und ihre Verwandten finden Anwendung in verschiedenen Bereichen:
- Physik: Modellierung von Küstenlinien, Oberflächenrauheit
- Computergrafik: Erzeugung natürlich aussehender Strukturen
- Antennentechnik: Fraktale Antennen mit kompakter Bauform
- Biologie: Modellierung von Blutgefäßen, Bronchien
- Wirtschaft: Analyse von Marktfluktuationen
- Kunst: Fraktale Kunst und Design
Verwandte Fraktale
Cantor-Menge
Eindimensionales Fraktal durch iterative Dreiteilung und Mittelentfernung.
Sierpinski-Dreieck
Zweidimensionales Fraktal mit ähnlicher Konstruktionslogik.
Dragon Curve
Fraktale Kurve durch wiederholte 90°-Faltungen.
Mandelbrot-Menge
Das berühmteste Fraktal, basierend auf komplexen Zahlen.
Philosophische Bedeutung
Die Koch Kurve illustriert wichtige Konzepte der modernen Mathematik und Philosophie:
- Paradoxien: Endliche Fläche mit unendlichem Umfang
- Skalenunabhängigkeit: Strukturen sehen auf allen Vergrößerungsebenen gleich aus
- Komplexität aus Einfachheit: Einfache Regeln erzeugen unendliche Komplexität
- Grenzwerte: Was passiert beim Übergang zum Unendlichen?
Praktische Berechnung
Für praktische Anwendungen wird die Koch Kurve nach einer endlichen Anzahl von Iterationen approximiert. Bereits nach wenigen Iterationen (n=3-5) sind die charakteristischen Eigenschaften deutlich erkennbar, während die Rechenzeit noch handhabbar bleibt.
|
|