Geradengleichung berechnen
Online Rechner und Formeln zur Berechnung der linearen Geradengleichung
Geradengleichung Rechner
Lineare Funktion
Die Geradengleichung f(x) = m·x + n beschreibt eine Gerade durch Steigung m und Y-Achsenabschnitt n.
Visualisierung
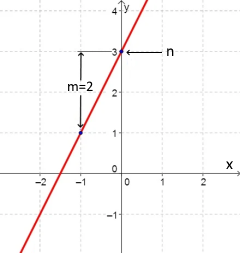
Die Grafik zeigt eine lineare Funktion f(x) = m·x + n.
Die Steigung m bestimmt die Neigung, n den Y-Achsenabschnitt.
Was ist eine Geradengleichung?
Eine Geradengleichung beschreibt eine gerade Linie in einem Koordinatensystem:
- Definition: f(x) = m·x + n (Normalform)
- Steigung m: Wie steil die Gerade verläuft
- Y-Achsenabschnitt n: Wo die Gerade die Y-Achse schneidet
- Anwendung: Beschreibung linearer Zusammenhänge
- Berechnung: Jeden beliebigen Parameter ermitteln
- Grafik: Eindeutige Darstellung einer Geraden
Wie funktioniert der Rechner?
Der Rechner löst die Geradengleichung nach dem gewählten Parameter auf:
Funktion berechnen
Bei gegebener Steigung m, X-Wert und Y-Achsenabschnitt n
Steigung berechnen
Bei gegebener Funktion, X-Wert und Y-Achsenabschnitt
Formeln zur Geradengleichung
Grundform der Geradengleichung
Normalform einer linearen Funktion
Steigung berechnen
Steigung aus Funktion, X-Wert und Y-Achsenabschnitt
X-Wert berechnen
X-Koordinate aus Funktion, Steigung und Y-Achsenabschnitt
Y-Achsenabschnitt berechnen
Y-Achsenabschnitt aus Funktion, Steigung und X-Wert
Beispiel
Gegeben
Berechnung von f(x)
Der Funktionswert beträgt 26
Bedeutung
- Steigung 4: Pro X-Einheit steigt Y um 4
- Y-Achsenabschnitt 6: Gerade schneidet Y-Achse bei 6
- Punkt (5,26): Liegt auf der Geraden
Anwendungen
Wirtschaft (Kosten-Erlös), Physik (gleichförmige Bewegung), Statistik (Regression).
Lineare Funktionen verstehen
Eine Geradengleichung ist eine mathematische Beschreibung einer geraden Linie in einem zweidimensionalen Koordinatensystem. Sie ist die einfachste Form einer Funktion und beschreibt einen linearen Zusammenhang zwischen zwei Variablen.
Die Normalform: f(x) = m·x + n
In der Normalform einer linearen Funktion haben die Parameter folgende Bedeutung:
- m (Steigung): Gibt an, um wie viele Einheiten der Y-Wert steigt oder fällt, wenn der X-Wert um 1 zunimmt
- n (Y-Achsenabschnitt): Gibt den Y-Wert an, bei dem die Gerade die Y-Achse schneidet (also bei x = 0)
- x (Variable): Die unabhängige Variable (Eingabewert)
- f(x) (Funktionswert): Die abhängige Variable (Ausgabewert)
Eigenschaften linearer Funktionen
Positive Steigung (m > 0)
Die Gerade steigt von links nach rechts an. Je größer m, desto steiler der Anstieg.
Negative Steigung (m < 0)
Die Gerade fällt von links nach rechts ab. Je kleiner m, desto steiler der Abfall.
Nullsteigung (m = 0)
Die Gerade verläuft horizontal. Der Funktionswert ist konstant: f(x) = n.
Y-Achsenabschnitt
Der Punkt (0, n) liegt immer auf der Geraden, unabhängig von der Steigung.
Praktische Anwendungen
Lineare Funktionen finden sich in vielen Bereichen des täglichen Lebens:
- Wirtschaft: Kosten-Erlös-Funktionen, Abschreibungen
- Physik: Gleichförmige Bewegung, Ohmsches Gesetz
- Alltagsmathematik: Handytarife, Mietkosten, Benzinverbrauch
- Statistik: Lineare Regression, Trendanalysen
|
|