Calculate Line Equation
Online calculator and formulas for calculating the linear line equation
Line Equation Calculator
Linear Function
The line equation f(x) = m·x + n describes a line through slope m and y-intercept n.
Visualization
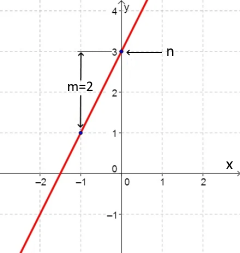
The graphic shows a linear function f(x) = m·x + n.
The slope m determines the inclination, n the y-intercept.
What is a Line Equation?
A line equation describes a straight line in a coordinate system:
- Definition: f(x) = m·x + n (standard form)
- Slope m: How steep the line runs
- Y-intercept n: Where the line intersects the Y-axis
- Application: Description of linear relationships
- Calculation: Determine any parameter
- Graph: Unique representation of a line
How Does the Calculator Work?
The calculator solves the line equation for the selected parameter:
Calculate Function
Given slope m, X-value and y-intercept n
Calculate Slope
Given function, X-value and y-intercept
Formulas for Line Equation
Basic Form of Line Equation
Standard form of a linear function
Calculate Slope
Slope from function, X-value and y-intercept
Calculate X-value
X-coordinate from function, slope and y-intercept
Calculate Y-intercept
Y-intercept from function, slope and X-value
Example
Given
Calculation of f(x)
The function value is 26
Meaning
- Slope 4: Y increases by 4 per X-unit
- Y-intercept 6: Line intersects Y-axis at 6
- Point (5,26): Lies on the line
Applications
Economics (cost-revenue), physics (uniform motion), statistics (regression).
Understanding Linear Functions
A line equation is a mathematical description of a straight line in a two-dimensional coordinate system. It is the simplest form of a function and describes a linear relationship between two variables.
The Standard Form: f(x) = m·x + n
In the standard form of a linear function, the parameters have the following meaning:
- m (slope): Indicates how many units the Y-value rises or falls when the X-value increases by 1
- n (y-intercept): Indicates the Y-value at which the line intersects the Y-axis (i.e., at x = 0)
- x (variable): The independent variable (input value)
- f(x) (function value): The dependent variable (output value)
Properties of Linear Functions
Positive Slope (m > 0)
The line rises from left to right. The larger m, the steeper the rise.
Negative Slope (m < 0)
The line falls from left to right. The smaller m, the steeper the fall.
Zero Slope (m = 0)
The line runs horizontally. The function value is constant: f(x) = n.
Y-intercept
The point (0, n) always lies on the line, regardless of the slope.
Practical Applications
Linear functions are found in many areas of daily life:
- Economics: Cost-revenue functions, depreciation
- Physics: Uniform motion, Ohm's law
- Everyday mathematics: Mobile phone tariffs, rent costs, fuel consumption
- Statistics: Linear regression, trend analysis
|
|