Ln, natural logarithm to base e

Calculator and formula for the natural logarithm to base e

Natural logarithm calculator

What is calculated?

The Ln function returns the natural logarithm to base e of the given number (power value). The argument must be a positive real number.

Input values


Result
The result is shown with the selected number of decimal places

Function graph

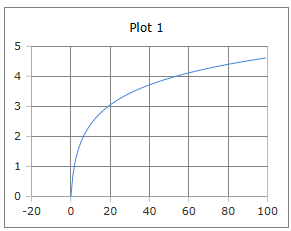
Natural logarithm graph

Graph of the natural logarithm function ln(x)

Natural logarithm info

Properties

Natural logarithm:

  • Base: e ≈ 2.71828
  • Domain: (0, ∞)
  • Range: (-∞, ∞)
  • Inverse function of e^x

Note: The natural logarithm is defined only for positive numbers. For complex numbers a separate function is available.

Special values
ln(1) = 0
Logarithm of 1 is always 0
ln(e) = 1
Logarithm of the base is 1
ln(e²) = 2
Logarithm of e² is 2
ln(1/e) = -1
Negative logarithm
Related functions

For complex numbers a separate Ln function is available: → Complex logarithm

Formulas of the natural logarithm

Definition
\[\ln(x) = \log_e(x)\] Logarithm to base e
Conversion
\[\ln(x) = \frac{\log(x)}{\log(e)}\] Change of base formula
Product rule
\[\ln(x \cdot y) = \ln(x) + \ln(y)\] Logarithm of a product
Power rule
\[\ln(x^a) = a \cdot \ln(x)\] Logarithm of a power
Quotient rule
\[\ln\left(\frac{x}{y}\right) = \ln(x) - \ln(y)\] Logarithm of a quotient
Derivative
\[\frac{d}{dx}\ln(x) = \frac{1}{x}\] Derivative of the natural logarithm

Calculation example

Example: calculate ln(20)

Given:

  • x = 20
  • Wanted: ln(20)

Calculation:

\[\ln(20) \approx 2.996\] \[\text{since } e^{2.996} \approx 20\]

Interpretation: 2.996 is the exponent to which the base e must be raised to obtain 20.

Practical example

Exponential growth

Problem:

A bacterial culture grows exponentially. After what time will the population double if the growth rate r = 0.693 per hour?

Solution:

\[2 = e^{0.693 \cdot t}\] \[\ln(2) = 0.693 \cdot t\] \[t = \frac{\ln(2)}{0.693} \approx 1 \text{ hour}\]

Definition and properties

Euler's number e

The base of the natural logarithm is Euler's number e ≈ 2.71828. It is one of the most important mathematical constants and appears in many natural growth processes.

Applications

The natural logarithm is used in many fields: compound interest, exponential growth and decay, information theory, statistics and probability.

Important properties
  • Domain: x > 0
  • Range: all real numbers
  • Monotonicity: strictly increasing
  • Continuity: continuous on (0, ∞)

Is this page helpful?            
Thank you for your feedback!

Sorry about that

How can we improve it?

More Exp, Log and Root functions

Exponential function base 10x  •  Exponential function base ex  •  Exponential function base xy  •  Modular Exponentiation (PowMod)  •  Logarithm to base 10 (Log)  •  Logarithm to base e (Ln)  •  Logarithm to base a (Loga)  •  Square root (sqrt)  •  Cubic root (cbrt)  •  nth root  •  Hypot  •