Ln, natürlicher Logarithmus zur Basis e

Rechner und Formel zur Berechnung des Logarithmus zur Basis e

Natürlicher Logarithmus Rechner

Was wird berechnet?

Die Funktion Ln liefert den natürlichen Logarithmus zur Basis e der angegebenen Zahl (Potenzwert). Als Argument muss eine positive reelle Zahl angegeben werden.

Eingabewerte


Ergebnis
Das Ergebnis wird mit der gewählten Anzahl Dezimalstellen angezeigt

Funktionsgraph

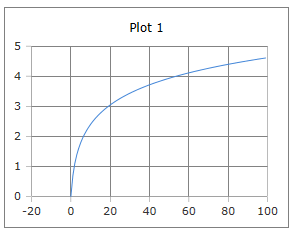
Natürlicher Logarithmus Graph

Graph der natürlichen Logarithmusfunktion ln(x)

Natürlicher Logarithmus Info

Eigenschaften

Natürlicher Logarithmus:

  • Basis: e ≈ 2.71828
  • Definitionsbereich: (0, ∞)
  • Wertebereich: (-∞, ∞)
  • Umkehrfunktion von e^x

Wichtig: Der natürliche Logarithmus ist nur für positive Zahlen definiert. Für komplexe Zahlen gibt es eine separate Funktion.

Spezielle Werte
ln(1) = 0
Logarithmus von 1 ist immer 0
ln(e) = 1
Logarithmus der Basis ergibt 1
ln(e²) = 2
Logarithmus von e² ergibt 2
ln(1/e) = -1
Negativer Logarithmus
Verwandte Funktionen

Für komplexe Zahlen steht eine separate Ln-Funktion zur Verfügung: → Komplexer Logarithmus

Formeln des natürlichen Logarithmus

Definition
\[\ln(x) = \log_e(x)\] Logarithmus zur Basis e
Umrechnung
\[\ln(x) = \frac{\log(x)}{\log(e)}\] Basiswechselformel
Produktregel
\[\ln(x \cdot y) = \ln(x) + \ln(y)\] Logarithmus eines Produkts
Potenzregel
\[\ln(x^a) = a \cdot \ln(x)\] Logarithmus einer Potenz
Quotientenregel
\[\ln\left(\frac{x}{y}\right) = \ln(x) - \ln(y)\] Logarithmus eines Quotienten
Ableitung
\[\frac{d}{dx}\ln(x) = \frac{1}{x}\] Ableitung des natürlichen Logarithmus

Rechenbeispiel

Beispiel: ln(20) berechnen

Gegeben:

  • x = 20
  • Gesucht: ln(20)

Berechnung:

\[\ln(20) \approx 2.996\] \[\text{da } e^{2.996} \approx 20\]

Interpretation: 2.996 ist der Exponent, den man für die Basis e benötigt, um 20 zu erhalten.

Praktisches Beispiel

Exponentielles Wachstum

Problem:

Eine Bakterienkultur wächst exponentiell. Nach welcher Zeit hat sich die Anzahl verdoppelt, wenn die Wachstumsrate r = 0.693 pro Stunde beträgt?

Lösung:

\[2 = e^{0.693 \cdot t}\] \[\ln(2) = 0.693 \cdot t\] \[t = \frac{\ln(2)}{0.693} \approx 1 \text{ Stunde}\]

Definition und Eigenschaften

Die Eulersche Zahl e

Die Basis des natürlichen Logarithmus ist die Eulersche Zahl e ≈ 2.71828. Sie ist eine der wichtigsten mathematischen Konstanten und tritt in vielen natürlichen Wachstumsprozessen auf.

Anwendungen

Der natürliche Logarithmus wird in vielen Bereichen verwendet: Zinseszinsrechnung, exponentielles Wachstum und Zerfall, Informationstheorie, Statistik und Wahrscheinlichkeitsrechnung.

Wichtige Eigenschaften
  • Definitionsbereich: x > 0
  • Wertebereich: alle reellen Zahlen
  • Monotonie: streng monoton steigend
  • Stetigkeit: stetig auf (0, ∞)

Ist diese Seite hilfreich?            
Vielen Dank für Ihr Feedback!

Das tut uns leid

Wie können wir die Seite verbessern?

Logarithmus und Exponenten

Log, Logarithmus zur Basis 10  •  Ln, Logarithmus zur Basis e  •  Logarithmus zur Basis a (Loga)  •  Exponential Funktion Basis 10x  •  Exponential Funktion Basis ex  •  Exponential Funktion Basis xy  •  Quadratwurzel  •  Kubikwurzel  •  N-te Wurzel  •  PowMod, Modular Exponentiation  •  Hypot  •