Überschlagenes Viereck berechnen
Rechner für selbstschneidende Vierecke
Überschlagenes Viereck Rechner
Das überschlagene Viereck
Ein überschlagenes Viereck entsteht durch Kreuzung zweier Seitenlinien und zeigt Selbstdurchdringung.
Überschlagene Struktur
Überschlagene Eigenschaften
Selbstschneidend: Zwei Seiten kreuzen sich im Inneren
Überschlagenes Viereck mit Kreuzung.
Zwei Seiten schneiden sich im Inneren.
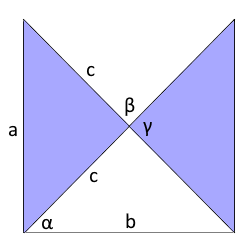
Das überschlagene Viereck: Geometrie der Selbstdurchdringung
Das überschlagene Viereck ist eine faszinierende Form der nicht-konvexen Geometrie:
- Selbstschneidend: Zwei Seitenlinien kreuzen sich
- Nicht-konvex: Innere Bereiche "falten" sich
- Kreuzungswinkel: Bestimmt durch Geometrie
- Besondere Schenkel: c = √(a²+b²)/2
- Einfache Fläche: A = (a×b)/2
- Winkel-Beziehungen: α = β/2
Besondere Eigenschaften der Überschlagung
Die geometrischen Eigenschaften sind durch die Selbstkreuzung geprägt:
Kreuzungs-Geometrie
- Zwei sich schneidende Seitenlinien
- Kreuzungspunkt im Inneren der Form
- Entstehung von vier Teilbereichen
- Nicht-konvexe Gesamtform
Winkel-System
- Kreuzungswinkel γ aus Cosinus-Formel
- Supplementwinkel β = 180° - γ
- Halbwinkel α = β/2
- Symmetrische Winkel-Beziehungen
Mathematik der Überschlagung
Die mathematischen Beziehungen sind trotz Komplexität elegant:
Schenkel-Berechnung
- c = √(a² + b²)/2
- Halbierte Diagonale des Rechtecks
- Pythagorischer Satz angewendet
- Charakteristische Halbierung
Flächen-Formel
- A = (a × b)/2
- Halbe Rechteck-Fläche
- Einfache Multiplikation
- Vorzeichenfragen bei Kreuzung
Anwendungen überschlagener Formen
Überschlagene Vierecke finden überraschende Anwendungen:
Mechanik & Kinematik
- Gelenkverbindungen mit Überkreuzung
- Pantograph-Mechanismen
- Scherengetriebe-Systeme
- Faltbare mechanische Strukturen
Design & Kunst
- Geometrische Muster und Ornamente
- Op-Art und visuelle Illusionen
- Architektonische Kreuzungs-Elemente
- Origami und Papierfalttechniken
Computergrafik
- Polygon-Triangulierung
- Self-Intersection Detection
- 3D-Modeling Algorithmen
- Game Engine Kollisions-Systeme
Mathematische Forschung
- Topologie nicht-konvexer Formen
- Knoten-Theorie Grundlagen
- Algebraische Geometrie
- Differentialgeometrie Studien
Formeln für das überschlagene Viereck
Schenkel c
Halbierte Rechteck-Diagonale
Flächeninhalt A
Halbe Rechteck-Fläche
Umfang U
Zweimal Basis plus viermal Schenkel
Kreuzungswinkel γ
Winkel an der Kreuzungsstelle
Winkel-Beziehungen
Supplementwinkel und Halbwinkel-Beziehung
Rechenbeispiel für ein überschlagenes Viereck
Gegeben
Gesucht: Alle Parameter des überschlagenen Vierecks
1. Schenkel berechnen
Halbierte Diagonale des entsprechenden Rechtecks
2. Fläche und Umfang
Halbe Rechteck-Fläche und Umfang-Berechnung
3. Winkel-Berechnungen
Kreuzungswinkel und Supplementwinkel
4. Vollständiges überschlagenes Viereck
Vollständige Kreuzungsgeometrie mit charakteristischen Winkeln!
Das überschlagene Viereck: Faszination der Selbstdurchdringung
Das überschlagene Viereck repräsentiert eine der interessantesten Formen der nicht-konvexen Geometrie. Diese selbstschneidende Struktur entsteht durch die Kreuzung zweier Seitenlinien und eröffnet faszinierende Einblicke in die Welt der komplexen geometrischen Beziehungen. Von mechanischen Anwendungen über künstlerische Gestaltung bis hin zur mathematischen Forschung zeigt das überschlagene Viereck, wie scheinbar einfache Transformationen zu überraschend komplexen und schönen Formen führen können.
Die Mathematik der Selbstkreuzung
Das überschlagene Viereck zeigt bemerkenswerte mathematische Eigenschaften:
- Elegante Schenkel-Formel: c = √(a²+b²)/2 - halbierte Rechteck-Diagonale
- Einfache Flächen-Berechnung: A = (a×b)/2 - halbe Rechteck-Fläche
- Kreuzungswinkel-Bestimmung: γ = arccos((2c²-a²)/(2c²))
- Winkel-Hierarchie: α = β/2 und β = 180°-γ
- Topologische Komplexität: Selbstschneidung erzeugt vier Teilbereiche
- Geometrische Dualität: Konvexe Eingabe, nicht-konvexe Ausgabe
Mechanische und technische Anwendungen
Überschlagene Strukturen finden vielfältige praktische Anwendungen:
Kinematische Systeme
Pantographen und Scherengetriebe nutzen überschlagene Geometrien für Bewegungsübertragung. Diese Mechanismen ermöglichen präzise Skalierung und Kraftverstärkung.
Faltbare Strukturen
Klappbare Tische, Scheren-Hubtische und faltbare Gerüste basieren auf überschlagenen Prinzipien. Die Selbstkreuzung ermöglicht kompakte Lagerung.
Robotik
Gelenkverbindungen mit Überkreuzung in Roboter-Armen ermöglichen erweiterte Bewegungsfreiheit. Parallelogramm-Mechanismen mit Kreuzung optimieren Arbeitsräume.
Textil-Industrie
Webmaschinen und Strick-Mechanismen nutzen überschlagene Fadenwege. Die Kreuzungsgeometrie ist fundamental für Textilherstellung.
Kunstgeschichte und Design
Die ästhetische Wirkung überschlagener Formen ist bemerkenswert:
- Optische Kunst: M.C. Escher und Op-Art-Künstler nutzten Selbstkreuzungen für visuelle Illusionen
- Islamische Ornamentik: Geometrische Muster mit überschlagenen Elementen
- Gotische Architektur: Kreuzrippen und überschlagene Gewölbestrukturen
- Moderne Skulptur: Minimalistische Arbeiten mit selbstschneidenden Formen
- Logo-Design: Überkreuzungen als Symbol für Verbindung und Integration
- Origami: Papierfalttechniken mit überschlagenen Zwischenstufen
Computergrafik und algorithmische Herausforderungen
Überschlagene Vierecke stellen die Computergrafik vor interessante Probleme:
Polygon-Verarbeitung
Self-Intersection Detection ist ein klassisches Problem der Computational Geometry. Algorithmen müssen Kreuzungspunkte effizient finden und behandeln.
Triangulierung
Überschlagene Polygone erfordern spezielle Triangulierungs-Algorithmen. Constrained Delaunay Triangulation wird oft verwendet.
Rendering
Überschlagene Formen können Z-Buffer-Konflikte verursachen. Order-Independent Transparency wird zur Lösung eingesetzt.
Kollisions-Erkennung
Game Engines müssen Kollisionen mit selbstschneidenden Objekten erkennen. Bounding Volume Hierarchies helfen bei der Effizienz.
Mathematische Forschung und Topologie
Das überschlagene Viereck eröffnet tiefe mathematische Fragen:
- Knoten-Theorie: Verbindungen zu mathematischen Knoten und Verschlingungen
- Algebraische Topologie: Homologie-Gruppen selbstschneidender Formen
- Differentialgeometrie: Krümmungsverhalten an Kreuzungspunkten
- Komplexe Analysis: Riemann-Flächen mit Verzweigungspunkten
- Kombinatorische Geometrie: Abzählprobleme für überschlagene Konfigurationen
- Optimierungstheorie: Minimierung von Selbstschnitten in Polygonen
Zusammenfassung
Das überschlagene Viereck demonstriert die faszinierende Komplexität, die aus einfachen geometrischen Transformationen entstehen kann. Durch die Selbstkreuzung zweier Seiten entsteht eine Form, die sowohl mathematisch elegant als auch praktisch vielseitig ist. Von den präzisen Formeln c = √(a²+b²)/2 und A = (a×b)/2 über mechanische Anwendungen in Pantographen bis hin zu künstlerischen Gestaltungen und computergrafischen Herausforderungen zeigt diese Form, wie Geometrie Grenzen zwischen Theorie und Praxis überwindet. Das überschlagene Viereck erinnert uns daran, dass die Schönheit der Mathematik oft in den unerwarteten Wendungen liegt - im wahrsten Sinne des Wortes. Es ist ein Symbol dafür, dass Komplexität und Einfachheit, Ordnung und Chaos, Eleganz und Überraschung in der Welt der geometrischen Formen harmonisch koexistieren können.
|
|