Drachenviereck berechnen

Online Rechner und Formeln zur Berechnung eines Drachenvierecks (Deltoid)

Drachenviereck Rechner

Drachenviereck-Parameter

Berechnet alle Parameter eines Drachenvierecks aus den Diagonalen e und f und der Distanz c.

Hauptdiagonale (Symmetrieachse)
Nebendiagonale (senkrecht zu e)
Abstand vom Zentrum
Ergebnisse
Seite a:
Seite b:
Umfang U:
Fläche A:
Winkel α:
Winkel γ:
Winkel β:

Visualisierung

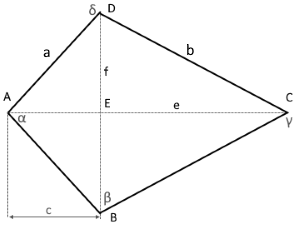
Drachenviereck

Das Diagramm zeigt ein Drachenviereck mit den Diagonalen e und f.
Die Diagonalen stehen senkrecht aufeinander und teilen die Fläche.

Was ist ein Drachenviereck?

Ein Drachenviereck (auch Deltoid genannt) ist ein spezielles Viereck mit besonderen Eigenschaften:

  • Definition: Zwei Paare gleich langer benachbarter Seiten
  • Symmetrie: Eine Hauptdiagonale als Symmetrieachse
  • Diagonalen: Stehen senkrecht aufeinander
  • Winkel: Gegenüberliegende Winkel sind gleich
  • Anwendung: Drachen, Fliesen, Kristallstrukturen
  • Berechnung: Aus Diagonalen und Position

Eigenschaften des Drachenvierecks

Das Drachenviereck hat charakteristische geometrische Eigenschaften:

Diagonalen
  • Diagonale e ist die Symmetrieachse
  • Diagonale f steht senkrecht zu e
  • Schnittpunkt teilt e im Verhältnis c:(e-c)
Winkel
  • Winkel α und γ liegen an der Symmetrieachse
  • Winkel β = δ (gegenüberliegende Winkel)
  • Summe aller Winkel beträgt 360°

Wie funktioniert die Berechnung?

Der Rechner verwendet die Diagonalen e und f sowie die Distanz c zur Berechnung:

Seitenlängen
\[a = \sqrt{\left(\frac{f}{2}\right)^2 + c^2}\]

Aus halber Diagonale f und Distanz c

Flächeninhalt
\[A = \frac{e \cdot f}{2}\]

Halbes Produkt der Diagonalen

Formeln zum Drachenviereck

Seite a
\[a = \sqrt{\left(\frac{f}{2}\right)^2 + c^2}\]

Erste Seitenlänge

Seite b
\[b = \sqrt{\left(\frac{f}{2}\right)^2 + (e-c)^2}\]

Zweite Seitenlänge

Flächeninhalt A
\[A = \frac{e \cdot f}{2}\]

Halbes Produkt der Diagonalen

Umfang U
\[U = 2 \cdot (a + b)\]

Summe aller vier Seiten

Winkel α
\[\alpha = \arccos\left(\frac{2a^2 - f^2}{2a^2}\right)\]

Winkel an der Spitze

Winkel γ
\[\gamma = \arccos\left(\frac{2b^2 - f^2}{2b^2}\right)\]

Gegenüberliegender Spitzenwinkel

Symbole und Bezeichnungen
  • e: Hauptdiagonale (Symmetrieachse)
  • f: Nebendiagonale (senkrecht zu e)
  • c: Distanz vom Zentrum zu einem Ende von e
  • a, b: Seitenlängen des Drachenvierecks
  • α, γ: Winkel an den Spitzen
  • β, δ: Seitenwinkel (β = δ)
  • A: Flächeninhalt
  • U: Umfang

Beispiel

Gegeben
e = 5 f = 4 c = 2
1. Seite a berechnen
\[a = \sqrt{(4/2)^2 + 2^2}\] \[a = \sqrt{4 + 4} = \sqrt{8} \approx 2.83\]

Erste Seitenlänge

2. Seite b berechnen
\[b = \sqrt{(4/2)^2 + (5-2)^2}\] \[b = \sqrt{4 + 9} = \sqrt{13} \approx 3.61\]

Zweite Seitenlänge

3. Fläche berechnen
\[A = \frac{5 \cdot 4}{2} = 10\]

Flächeninhalt in Quadrateinheiten

4. Umfang berechnen
\[U = 2 \cdot (2.83 + 3.61) \approx 12.8\]

Gesamtumfang

Das Drachenviereck in Mathematik und Alltag

Ein Drachenviereck oder Deltoid ist ein Viereck, das zwei Paare gleich langer benachbarter Seiten besitzt. Es ist nach seiner charakteristischen Form benannt, die an einen Drachen erinnert. Das Drachenviereck ist ein wichtiges geometrisches Objekt mit interessanten mathematischen Eigenschaften und praktischen Anwendungen.

Mathematische Definition

Ein Drachenviereck ist definiert durch:

  • Seitenlängen: Zwei Paare benachbarter Seiten gleicher Länge (a = a und b = b)
  • Symmetrie: Eine Diagonale als Symmetrieachse
  • Diagonalen: Stehen senkrecht aufeinander
  • Winkel: Gegenüberliegende Winkel an den "Seitenspitzen" sind gleich

Geometrische Eigenschaften

Diagonalen

Die Hauptdiagonale e ist die Symmetrieachse und wird von der Nebendiagonale f senkrecht geschnitten.

Flächenberechnung

Die Fläche ist das halbe Produkt der beiden Diagonalen: A = (e × f) / 2.

Winkel

Die Winkel α und γ liegen an den Spitzen der Symmetrieachse, β und δ sind die seitlichen Winkel.

Symmetrie

Das Drachenviereck ist spiegelsymmetrisch bezüglich der Hauptdiagonale e.

Anwendungen und Beispiele

Drachenvierecke finden sich in vielen Bereichen:

  • Natur: Kristallstrukturen, Blattformen, Tiermuster
  • Architektur: Fensterformen, Bodenfliesen, Dachkonstruktionen
  • Design: Logos, Schmuck, Ornamente
  • Spiele: Drachen, Spielzeug, Puzzles
  • Technik: Gelenkverbindungen, Mechanismen

Spezielle Formen

Rechtwinkliges Deltoid

Ein Drachenviereck mit einem rechten Winkel an einer der Seitenspitzen.

Rhombus

Sonderfall eines Drachenvierecks, bei dem alle vier Seiten gleich lang sind.

Quadrat

Spezieller Rhombus mit vier rechten Winkeln.

Konkaves Deltoid

Drachenviereck mit einem einspringenden Winkel (größer als 180°).

Konstruktion und Berechnung

Ein Drachenviereck kann auf verschiedene Weise konstruiert und berechnet werden:

  • Aus Diagonalen: Gegeben sind die beiden Diagonalen und ihre Lage zueinander
  • Aus Seitenlängen: Gegeben sind die Längen der beiden Seitenpaare
  • Aus Winkeln: Gegeben sind bestimmte Winkel und eine Seitenlänge
  • Aus Flächeninhalt: Rückrechnung aus Fläche und anderen Parametern

Verwandte Vierecke

Das Drachenviereck gehört zur Familie der Vierecke und hat Beziehungen zu:

  • Parallelogramm: Gegenüberliegende Seiten sind parallel und gleich
  • Trapez: Ein Paar paralleler Seiten
  • Rhombus: Spezialfall des Drachenvierecks
  • Rechteck: Parallelogramm mit rechten Winkeln

Ist diese Seite hilfreich?            
Vielen Dank für Ihr Feedback!

Das tut uns leid

Wie können wir die Seite verbessern?


Weitere Viereck Funktionen

Quadrat • Rechteck • Goldenes Rechteck • Rechteck und Quadrat • Parallelogramm • Parallelogramm Flächeninhalt • Raute • Raute Flächeninhalt • Allgemeines Viereck • Sehnenviereck • Konkaves Viereck • Pfeilviereck • Überschlagenes Viereck • Rahmen • Drachenviereck • Drachenviereck Flächeninhalt • Drachenviereck, Halbquadrat • Drachenviereck, rechtwinklig