Rechtwinkliges Deltoid berechnen
Rechner und Formeln für ein Drachenviereck mit zwei gegenüberliegenden rechten Winkeln
Rechtwinkliges Deltoid Rechner
Besonderes Drachenviereck
Ein rechtwinkliges Deltoid hat zwei gegenüberliegende rechte Winkel zwischen den kurzen und langen Seiten - ähnlich einem Rechteck mit variabler Form.
Visualisierung
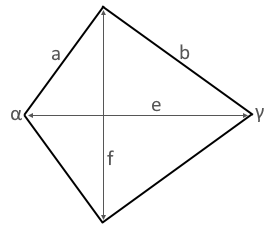
Das Diagramm zeigt ein rechtwinkliges Deltoid mit zwei 90°-Winkeln.
Die gegenüberliegenden rechten Winkel verleihen besondere Eigenschaften.
Was ist ein rechtwinkliges Deltoid?
Ein rechtwinkliges Deltoid ist ein spezielles Drachenviereck mit einzigartigen Eigenschaften:
- Zwei rechte Winkel: Gegenüberliegende Ecken haben jeweils 90°
- Drachenviereck: Zwei Paare gleich langer benachbarter Seiten
- Symmetrieachse: Eine Diagonale teilt die Form symmetrisch
- Rechteck-ähnlich: Kombiniert Rechteck- und Dracheneigenschaften
- Anwendung: Architektur, Fensterformen, Design
- Berechnung: Vereinfachte Formeln durch rechte Winkel
Zwei gegenüberliegende rechte Winkel
Die zwei rechten Winkel machen dieses Deltoid zu etwas Besonderem:
Rechte Winkel
- Liegen an gegenüberliegenden Ecken
- Zwischen kurzen und langen Seiten
- Bilden eine "Rechteck-ähnliche" Struktur
Vereinfachte Formeln
- Flächeninhalt A = a × b
- Diagonale e = √(a² + b²)
- Einfache Winkelbeziehungen
Ähnlichkeit mit einem Rechteck
Das rechtwinklige Deltoid vereint Rechteck- und Dracheneigenschaften:
Wie ein Rechteck
- Zwei rechte Winkel
- Flächeninhalt A = a × b
- Konstruierbar mit Rechteck
Wie ein Drachen
- Zwei Paar gleiche Seiten
- Senkrechte Diagonalen
- Eine Symmetrieachse
Einzigartig
- Kombination beider Eigenschaften
- Besondere mathematische Beziehungen
- Vielseitige Anwendbarkeit
Besondere Eigenschaften
Das rechtwinklige Deltoid hat charakteristische Eigenschaften:
Diagonalen
- Diagonale e ist die Symmetrieachse
- Diagonale f steht senkrecht zu e
- e = √(a² + b²) (Pythagoras)
- f = 2ab/e (spezielle Beziehung)
Winkel
- Zwei Winkel = 90° (gegenüberliegend)
- Winkel α und γ ergänzen sich zu 180°
- Symmetrische Anordnung
- Einfache Beziehungen untereinander
Formeln zum rechtwinkligen Deltoid
Flächeninhalt A
Einfachste Formel - wie beim Rechteck!
Umfang U
Standard-Drachenviereck-Formel
Diagonale e
Pythagoras - durch rechte Winkel!
Diagonale f
Spezielle Beziehung im rechtwinkligen Fall
Inkreisradius rᵢ
Harmonisches Mittel der Seiten
Umkreisradius rc
Halbe Hauptdiagonale
Winkelformeln
Besonderheit: Zwei Winkel sind fest bei 90°, die anderen beiden ergänzen sich zu 180°.
Symbole und Bezeichnungen
- a, b: Die beiden verschiedenen Seitenlängen
- e: Hauptdiagonale (Symmetrieachse)
- f: Nebendiagonale (senkrecht zu e)
- 90°: Die beiden rechten Winkel (fest)
- α, γ: Die beiden variablen Winkel
- rᵢ: Innenkreisradius
- rc: Umkreisradius
- A: Flächeninhalt, U: Umfang
Rechenbeispiel
Gegeben
1. Fläche berechnen
Einfache Multiplikation - wie beim Rechteck!
2. Diagonale e berechnen
Pythagoras durch die rechten Winkel
3. Umfang berechnen
Standard-Drachenviereck-Formel
4. Besonderheiten
- Zwei 90°-Winkel: Fest vorgegeben
- Rechteck-ähnlich: A = a × b
- Pythagoras anwendbar: Für Diagonale e
Das rechtwinklige Deltoid in Mathematik und Praxis
Ein rechtwinkliges Deltoid ist eine faszinierende geometrische Form, die die Eigenschaften eines Drachenvierecks mit denen eines Rechtecks kombiniert. Die beiden gegenüberliegenden rechten Winkel verleihen dieser Form einzigartige mathematische Eigenschaften und praktische Anwendungsmöglichkeiten.
Definition und Besonderheiten
Ein rechtwinkliges Deltoid ist definiert durch:
- Drachenviereck-Eigenschaften: Zwei Paare gleich langer benachbarter Seiten
- Zwei rechte Winkel: An gegenüberliegenden Ecken, jeweils zwischen unterschiedlichen Seitenlängen
- Position der rechten Winkel: Zwischen den kurzen und langen Seiten
- Symmetrie: Eine Diagonale bleibt die Symmetrieachse
Mathematische Vereinfachungen
Die beiden rechten Winkel führen zu bemerkenswerten Vereinfachungen:
Flächenberechnung
Die einfache Formel A = a × b macht die Flächenberechnung so einfach wie bei einem Rechteck.
Pythagoras anwendbar
Die Hauptdiagonale e kann direkt mit e = √(a² + b²) berechnet werden.
Konstruktion
Kann einfach aus einem Rechteck durch "Knicken" an der Mittellinie konstruiert werden.
Symmetrie
Trotz der rechten Winkel bleibt die charakteristische Drachenviereck-Symmetrie erhalten.
Praktische Anwendungen
Rechtwinklige Deltoide finden vielfältige Anwendung:
- Architektur: Spezielle Fensterformen, asymmetrische aber strukturierte Designs
- Handwerk: Fliesen mit besonderen Passformen für komplexe Muster
- Technik: Gelenkverbindungen mit definierten rechtwinkligen Positionen
- Design: Logos und grafische Elemente mit strukturierter Asymmetrie
- Möbeldesign: Tischplatten und andere Oberflächen mit charakteristischer Form
Geometrische Beziehungen
Zu Rechtecken
Teilt die Eigenschaft A = a × b und die Anwendbarkeit des Pythagoras für die Diagonale.
Zu Drachenvierecken
Behält die charakteristischen Eigenschaften: gleiche benachbarte Seiten, senkrechte Diagonalen, Symmetrieachse.
Zu Quadraten
Wird zu einem Quadrat, wenn a = b (dann sind alle vier Winkel rechte Winkel).
Zu Rauten
Verwandtschaft durch die gemeinsamen Drachenviereck-Eigenschaften, aber unterschiedliche Winkelkonstellation.
Konstruktionsmethoden
Ein rechtwinkliges Deltoid kann auf verschiedene Weise konstruiert werden:
- Aus den Seitenlängen: Zeichnen Sie die beiden Seitenlängen mit rechten Winkeln an den entsprechenden Ecken
- Aus einem Rechteck: "Knicken" Sie ein Rechteck entlang einer Mittellinie
- Über die Diagonalen: Nutzen Sie e = √(a² + b²) und die senkrechte Eigenschaft
- Symmetrische Konstruktion: Spiegeln Sie ein rechtwinkliges Dreieck an der geeigneten Seite
Besondere Eigenschaften im Detail
Das rechtwinklige Deltoid zeigt interessante mathematische Eigenschaften:
- Flächeneffizienz: Maximale Fläche bei gegebenen Seitenlängen (wie beim Rechteck)
- Diagonale-Verhältnisse: Spezielle Beziehung zwischen den beiden Diagonalen
- Inkreis und Umkreis: Beide existieren mit einfach berechenbaren Radien
- Symmetrieachse: Die Hauptdiagonale teilt nicht nur die Form, sondern auch die Fläche exakt
- Winkelkonstellation: Zwei feste 90°-Winkel, zwei variable Winkel mit α + γ = 180°
Historische und kulturelle Bedeutung
Diese geometrische Form erscheint in verschiedenen kulturellen Kontexten:
- Islamische Kunst: In komplexen geometrischen Mustern und Ornamenten
- Moderne Architektur: Als Gestaltungselement für dynamische aber strukturierte Formen
- Mathematische Bildung: Als Beispiel für die Kombination verschiedener geometrischer Eigenschaften
- Industriedesign: Für funktionale Formen mit ästhetischen Qualitäten
Zusammenfassung
Das rechtwinklige Deltoid ist ein perfektes Beispiel dafür, wie die Kombination verschiedener geometrischer Eigenschaften zu einer Form mit sowohl praktischen als auch ästhetischen Qualitäten führt. Es vereint die Einfachheit der Rechteck-Berechnung mit der Eleganz der Drachenviereck-Symmetrie.
|
|