Halbquadrat-Deltoid berechnen
Rechner und Formeln für ein spezielles Drachenviereck mit rechtem Winkel
Halbquadrat-Deltoid Rechner
Spezielles Drachenviereck
Ein Halbquadrat-Deltoid ist ein Drachenviereck mit einem rechten Winkel an einer der nicht-symmetrischen Ecken.
Visualisierung
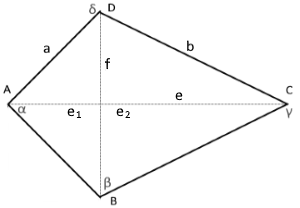
Das Diagramm zeigt ein Halbquadrat-Deltoid mit rechtem Winkel.
Eine Ecke hat einen 90°-Winkel, was diese Form besonders macht.
Was ist ein Halbquadrat-Deltoid?
Ein Halbquadrat-Deltoid ist ein spezielles Drachenviereck mit besonderen Eigenschaften:
- Rechter Winkel: Eine der nicht-symmetrischen Ecken hat 90°
- Drachenviereck: Zwei Paare gleich langer benachbarter Seiten
- Symmetrieachse: Eine Diagonale teilt die Form symmetrisch
- Spezialfall: Vereinfacht viele Berechnungen
- Anwendung: Architektur, Design, Handwerk
- Eigenschaften: Kombiniert Rechteck- und Dracheneigenschaften
Der rechte Winkel macht den Unterschied
Der rechte Winkel verleiht diesem Deltoid besondere mathematische Eigenschaften:
Rechter Winkel
- Liegt an einer der seitlichen Ecken
- Vereinfacht die Flächenberechnung
- Ermöglicht einfache Konstruktion
Vereinfachte Formeln
- Diagonale f = √2 × a
- Einfache Winkelbeziehungen
- Direkte Flächenberechnung möglich
Besondere Eigenschaften
Das Halbquadrat-Deltoid vereint Eigenschaften verschiedener geometrischer Formen:
Drachenviereck
- Zwei Paar gleiche Seiten
- Senkrechte Diagonalen
- Eine Symmetrieachse
Rechtwinkligkeit
- Ein Winkel = 90°
- Vereinfachte Berechnungen
- Besondere Symmetrien
Messbarkeit
- Aus zwei Seiten berechenbar
- Alle Parameter ableitbar
- Einfache Konstruktion
Wie funktioniert die Berechnung?
Aus den beiden Seitenlängen a und b werden alle anderen Parameter berechnet:
Flächeninhalt
Spezielle Formel für Halbquadrat-Deltoid
Diagonale f
Vereinfachte Formel durch rechten Winkel
Formeln zum Halbquadrat-Deltoid
Flächeninhalt A
Spezialformel für rechtwinkliges Deltoid
Umfang U
Summe aller vier Seiten
Diagonale f
Vereinfacht durch rechten Winkel
Diagonale e
Hauptdiagonale (Symmetrieachse)
Winkel β
Berechnung aus γ-Winkel
Winkel γ
Spitzenwinkel gegenüber dem rechten Winkel
Symbole und Bezeichnungen
- a, b: Die beiden verschiedenen Seitenlängen
- e: Hauptdiagonale (Symmetrieachse)
- f: Nebendiagonale (senkrecht zu e)
- e₁, e₂: Abschnitte der Hauptdiagonale
- β, γ: Die beiden verschiedenen Winkel
- 90°: Der rechte Winkel (fest)
- rᵢ: Innenkreisradius
- A: Flächeninhalt, U: Umfang
Rechenbeispiel
Gegeben
1. Diagonale f berechnen
Einfache Formel durch rechten Winkel
2. Umfang berechnen
Standardformel für Drachenviereck
3. Besonderheiten
- Rechter Winkel: Vereinfacht Berechnungen
- Symmetrie: Zwei gleiche Winkel β
- Konstruktion: Einfach mit Zirkel und Lineal
Das Halbquadrat-Deltoid in Mathematik und Praxis
Ein Halbquadrat-Deltoid ist ein faszinierender Spezialfall des Drachenvierecks, der durch die Kombination eines rechten Winkels mit den typischen Eigenschaften eines Deltoids entstteht. Diese Kombination führt zu vereinfachten mathematischen Beziehungen und interessanten geometrischen Eigenschaften.
Definition und Charakteristika
Ein Halbquadrat-Deltoid ist definiert durch:
- Drachenviereck-Eigenschaften: Zwei Paare gleich langer benachbarter Seiten
- Rechter Winkel: Eine der vier Ecken hat exakt 90°
- Position des rechten Winkels: Liegt an einer der "seitlichen" Ecken (nicht an der Spitze)
- Symmetrie: Eine Diagonale bleibt die Symmetrieachse
Mathematische Vereinfachungen
Der rechte Winkel führt zu erheblichen Vereinfachungen in den Formeln:
Diagonale f
Die einfache Beziehung f = √2 × a macht viele Berechnungen direkter.
Winkelbeziehungen
Die Winkel stehen in festen Beziehungen zueinander, was die Berechnung erleichtert.
Flächenberechnung
Spezielle Formeln nutzen die rechtwinklige Struktur für effiziente Berechnungen.
Konstruktion
Der rechte Winkel ermöglicht einfache geometrische Konstruktionen.
Praktische Anwendungen
Halbquadrat-Deltoide finden sich in verschiedenen Bereichen:
- Architektur: Fensterformen, Dachkonstruktionen mit besonderen Anforderungen
- Design: Logos und grafische Elemente mit asymmetrischer Balance
- Handwerk: Fliesen und Mosaiksteine mit speziellen Passformen
- Technik: Gelenkverbindungen mit definierten Bewegungsbereichen
- Kunst: Skulpturen und abstrakte Formen
Besondere Eigenschaften
Symmetrie
Trotz des asymmetrisch wirkenden rechten Winkels bleibt eine Symmetrieachse erhalten.
Stabilität
Der rechte Winkel verleiht der Form strukturelle Vorteile in konstruktiven Anwendungen.
Berechenbarkeit
Aus nur zwei Parametern (den Seitenlängen) lassen sich alle anderen Größen ableiten.
Verwandtschaft
Verbindet Eigenschaften von Rechtecken, Dreiecken und allgemeinen Drachenvierecken.
Konstruktion und Zeichnung
Ein Halbquadrat-Deltoid kann auf verschiedene Weise konstruiert werden:
- Ausgehend von den Seiten: Zeichnen Sie die beiden ungleichen Seitenlängen mit einem rechten Winkel
- Über die Diagonalen: Nutzen Sie die bekannte Beziehung f = √2 × a
- Symmetriekonstruktion: Spiegeln Sie ein rechtwinkliges Dreieck an einer Seite
- Koordinatensystem: Platzieren Sie die Eckpunkte systematisch im kartesischen System
Vergleich mit verwandten Formen
Das Halbquadrat-Deltoid steht in Beziehung zu anderen geometrischen Formen:
- Allgemeines Drachenviereck: Spezialisierung durch den rechten Winkel
- Rechteck: Teilt die Eigenschaft rechter Winkel, aber andere Seitenverhältnisse
- Rhombus: Verwandt, aber ohne die spezielle Winkelkonstellation
- Rechtwinkliges Dreieck: Ähnliche trigonometrische Beziehungen
Zusammenfassung
Das Halbquadrat-Deltoid ist ein elegantes Beispiel dafür, wie eine einzige zusätzliche Bedingung (der rechte Winkel) eine ganze Familie von geometrischen Eigenschaften und vereinfachten Berechnungsmethoden ermöglicht.
|
|