Allgemeines Viereck berechnen
Rechner und Formeln zur Berechnung der Eigenschaften eines allgemeines Vierecks
Diese Funktion berechnet verschiedene Eigenschaften eines allgemeinen Vierecks.
Zur Berechnung geben Sie die Längen von 3 Seiten und die beiden Winkel ein, die diese Seiten verbinden. Dann klicken Sie auf den Button 'Berechnen'.
|
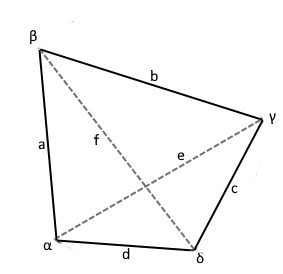
Formeln zum allgemeinen Viereck
Diagonale (e)
\(\displaystyle e =\sqrt{a^2+b^2-2ab·cos(β)} \)
Diagonale (f)
\(\displaystyle f =\sqrt{b^2+c^2-2bc·cos(γ)} \)
Flächeninhalt (A)
gegeben a, b, c, d, e, f
\(\displaystyle A=\frac{\sqrt{4e^2f^2-(b^2+d^2-a^2-c^2)^2}}{4}\)
gegeben a, b, c, d, α, δ
\(\displaystyle A=\sqrt{(s-a)(s-b)(s-c)(s-d)-abcd·cos^2\left(\frac{α+γ}{2} \right)} \)
\(\displaystyle s=\frac{a+b+c+d}{2} \)
Umfang (U)
\(\displaystyle U=a+b+c+d\)
Winkel (α)
\(\displaystyle α=arccos\left(\frac{a^2+d^2-f^2}{2ad} \right)\)
Winkel (δ)
\(\displaystyle δ=360°-α-β-γ\)
Seite (d)
\(\displaystyle d=\sqrt{c^2+e^2-2ce·cos(γ_2)}\)
\(\displaystyle γ_2=γ-γ_1\)
\(\displaystyle γ_1=arcos\left(\frac{b^2+e^2-a^2}{2be}\right)\)

Weitere Viereck Funktionen
Quadrat • Rechteck • Goldenes Rechteck • Rechteck und Quadrat • Parallelogramm • Parallelogramm Flächeninhalt • Raute • Raute Flächeninhalt • Allgemeines Viereck • Sehnenviereck • Konkaves Viereck • Pfeilviereck • Überschlagenes Viereck • Rahmen • Drachenviereck • Drachenviereck Flächeninhalt • Drachenviereck, Halbquadrat • Drachenviereck, rechtwinklig
|
|