Drachenviereck Flächeninhalt berechnen
Online Rechner zur Berechnung des Flächeninhalts eines Drachenvierecks
Flächeninhalt Rechner
Flächenberechnung
Berechnet die Fläche A eines Drachenvierecks aus den beiden Diagonalen e und f mit der einfachen Formel A = (e × f) / 2.
Visualisierung
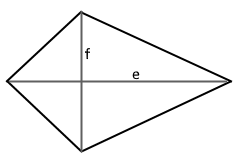
Das Diagramm zeigt die beiden Diagonalen e und f eines Drachenvierecks.
Die Fläche berechnet sich als halbes Produkt der Diagonalen.
Flächeninhalt eines Drachenvierecks
Der Flächeninhalt eines Drachenvierecks lässt sich sehr einfach berechnen:
- Formel: A = (e × f) / 2
- Diagonalen: Stehen senkrecht aufeinander
- Berechnung: Halbes Produkt der Diagonalen
- Einheit: Quadrateinheiten (z.B. cm², m²)
- Anwendung: Flächenberechnungen in der Geometrie
- Vorteil: Sehr einfache und direkte Formel
Die Flächenformel
Die Flächenformel für ein Drachenviereck ist eine der einfachsten in der Geometrie:
A = Flächeninhalt, e = erste Diagonale, f = zweite Diagonale
Warum funktioniert das?
Die Diagonalen teilen das Drachenviereck in vier rechtwinklige Dreiecke. Die Gesamtfläche ist das halbe Produkt der Diagonalen.
Wichtiger Hinweis
Diese Formel gilt nur, wenn die Diagonalen senkrecht aufeinander stehen, was bei Drachenvierecken immer der Fall ist.
Schritt-für-Schritt Berechnung
So berechnen Sie die Fläche eines Drachenvierecks:
Schritt 1
Messen Sie beide Diagonalen e und f
Schritt 2
Multiplizieren Sie e × f
Schritt 3
Teilen Sie das Ergebnis durch 2
Rechenbeispiel
Gegeben
Berechnung
Die Fläche beträgt 12 Quadratzentimeter
Schritt-für-Schritt
- Diagonalen: e = 6 cm, f = 4 cm
- Multiplizieren: 6 × 4 = 24
- Halbieren: 24 ÷ 2 = 12 cm²
Anwendungen
Praktische Anwendungen
- Architektur: Flächenberechnung von Fenstern
- Handwerk: Materialberechnung für Fliesen
- Garten: Beetflächen planen
- Design: Grafische Elemente
Verwandte Berechnungen
- Umfang: Benötigt zusätzlich die Seitenlängen
- Winkel: Berechnung aus Diagonalen möglich
- Seitenlängen: Aus Diagonalen ableitbar
Vollständige Berechnung
Für alle Parameter eines Drachenvierecks nutzen Sie den vollständigen Drachenviereck-Rechner .
Flächenberechnung bei Drachenvierecken
Die Flächenberechnung eines Drachenvierecks gehört zu den einfachsten Berechnungen in der Geometrie. Die Formel A = (e × f) / 2 ist nicht nur elegant, sondern auch sehr praktisch anwendbar.
Warum ist die Formel so einfach?
Die Einfachheit der Formel liegt in der besonderen Eigenschaft des Drachenvierecks:
- Senkrechte Diagonalen: Die beiden Diagonalen stehen immer im rechten Winkel zueinander
- Symmetrie: Eine Diagonale ist die Symmetrieachse des Drachenvierecks
- Zerlegung: Die Diagonalen teilen das Viereck in vier rechtwinklige Dreiecke
- Addition: Die Summe der vier Dreiecksflächen ergibt die Gesamtfläche
Mathematische Herleitung
Die Formel kann mathematisch einfach hergeleitet werden:
- Das Drachenviereck wird durch die Diagonalen in 4 rechtwinklige Dreiecke geteilt
- Jedes Dreieck hat die Fläche: A_Dreieck = (1/2) × Kathete1 × Kathete2
- Die Katheten sind jeweils Teile der Diagonalen e und f
- Die Summe aller vier Dreiecke ergibt: A_gesamt = (e × f) / 2
Praktische Tipps
Messgenauigkeit
Je genauer Sie die Diagonalen messen, desto präziser wird das Ergebnis.
Einheiten beachten
Die Flächeneinheit ist immer das Quadrat der Längeneinheit (cm → cm²).
Rechenkontrolle
Überprüfen Sie das Ergebnis durch eine alternative Berechnung oder Schätzung.
Plausibilität
Die Fläche sollte kleiner sein als das umschreibende Rechteck (e × f).
Vergleich mit anderen Vierecken
Die Flächenberechnung des Drachenvierecks unterscheidet sich von anderen Vierecken:
- Rechteck: A = Länge × Breite
- Parallelogramm: A = Grundseite × Höhe
- Trapez: A = (a + c) × h / 2
- Drachenviereck: A = (e × f) / 2 (einfachste Formel!)
Wichtiger Hinweis
Diese Formel gilt nur für Drachenvierecke! Bei anderen Vierecken mit nicht-senkrechten Diagonalen muss eine andere Formel verwendet werden.
|
|