Parallelogramm Flächeninhalt berechnen
Rechner und Formeln zur Berechnung des Flächeninhalts eines Parallelogramms
Parallelogramm Rechner
Parallelogramm Flächenberechnung
Ein Parallelogramm hat parallele Gegenseiten und die Fläche A = Basis × Höhe. Einfache und präzise Berechnung.
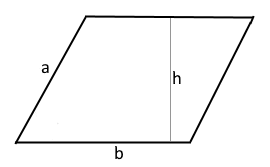
Parallelogramm Visualisierung
Das Diagramm zeigt ein Parallelogramm mit Basis b und Höhe h.
Die Fläche berechnet sich als A = b × h.
Was ist ein Parallelogramm?
Ein Parallelogramm ist ein Viereck mit besonderen Eigenschaften:
- Parallele Seiten: Gegenüberliegende Seiten sind parallel
- Gleiche Seitenlängen: Gegenüberliegende Seiten sind gleich lang
- Gleiche Winkel: Gegenüberliegende Winkel sind gleich
- Flächenberechnung: A = Basis × Höhe
- Höhe: Senkrechter Abstand zwischen parallelen Seiten
- Anwendungen: Technik, Architektur, Physik
Eigenschaften des Parallelogramms
Das Parallelogramm hat charakteristische geometrische Eigenschaften:
Seiten und Winkel
- Gegenüberliegende Seiten sind parallel und gleich lang
- Gegenüberliegende Winkel sind gleich
- Benachbarte Winkel ergänzen sich zu 180°
- Winkelsumme beträgt 360°
Diagonalen
- Diagonalen halbieren sich gegenseitig
- Diagonalen teilen das Parallelogramm in 4 Dreiecke
- Gegenüberliegende Dreiecke sind kongruent
- Diagonalen sind im Allgemeinen nicht gleich lang
Flächenberechnung verstehen
Die Flächenberechnung des Parallelogramms basiert auf einem einfachen Prinzip:
Das Grundprinzip
- Basis b: Eine der parallelen Seiten
- Höhe h: Senkrechter Abstand zur Basis
- Formel: A = b × h
- Höhe ist nicht gleich der Seitenlänge!
Warum funktioniert das?
- Parallelogramm lässt sich zu Rechteck umformen
- Fläche bleibt dabei unverändert
- Rechteckfläche = Länge × Breite
- Entspricht Basis × Höhe des Parallelogramms
Anwendungen von Parallelogrammen
Parallelogramme finden sich in vielen praktischen Bereichen:
Architektur & Bauwesen
- Dachkonstruktionen und Träger
- Fenster- und Türrahmen
- Fassadenelemente
- Treppen und Rampen
Maschinenbau & Technik
- Getriebe und Mechanismen
- Parallelogrammlenker
- Scherenhubtische
- Pantograph-Konstruktionen
Design & Kunst
- Grafische Gestaltung
- Logos und Corporate Design
- Muster und Ornamente
- Moderne Architektur
Mathematik & Physik
- Vektordarstellung
- Kräfteparallelogramm
- Koordinatentransformation
- Gitterstrukturen
Formeln für das Parallelogramm
Flächeninhalt A
Basis mal Höhe (senkrechter Abstand)
Basis aus Fläche
Basis berechnen wenn Fläche und Höhe bekannt
Höhe aus Fläche
Höhe berechnen wenn Fläche und Basis bekannt
Alternative Flächenformel
Mit Seitenlängen a, b und Winkel α
Wichtige Hinweise
- b: Basis (eine der Seiten)
- h: Höhe (senkrecht zur Basis)
- A: Flächeninhalt
- α: Winkel zwischen den Seiten
- Höhe ≠ Seitenlänge (außer bei Rechteck)
- Höhe: Immer senkrecht zur gewählten Basis
Rechenbeispiel für ein Parallelogramm
Gegeben
Gesucht: Flächeninhalt des Parallelogramms
1. Formel anwenden
Einfache Multiplikation von Basis und Höhe
2. Ergebnis interpretieren
Das Parallelogramm hat eine Fläche von 40 Einheiten²
3. Kontrolle und Verständnis
Die Umkehrprüfung bestätigt unser Ergebnis
Das Parallelogramm: Fundamentale Form der Geometrie
Das Parallelogramm ist eine der wichtigsten und vielseitigsten geometrischen Formen. Es vereint mathematische Eleganz mit praktischer Anwendbarkeit und bildet die Grundlage für das Verständnis komplexerer geometrischer Strukturen und physikalischer Prinzipien.
Mathematische Grundlagen und Eigenschaften
Die mathematischen Eigenschaften des Parallelogramms sind vielfältig und elegant:
- Parallelität: Gegenüberliegende Seiten sind parallel und gleich lang
- Winkeleigenschaften: Gegenüberliegende Winkel sind gleich, benachbarte ergänzen sich
- Diagonalen: Schneiden sich in der Mitte und teilen sich gegenseitig
- Symmetrie: Punktsymmetrisch zum Schnittpunkt der Diagonalen
- Flächenformel: A = Basis × Höhe (unabhängig von der Schräge)
- Vektordarstellung: Ideal für die Darstellung von Vektoren
Die Flächenberechnung verstehen
Die Flächenformel A = b × h ist eleganter als sie zunächst erscheint:
Geometrische Intuition
Jedes Parallelogramm lässt sich durch "Scherung" in ein flächengleiches Rechteck überführen. Die Höhe bleibt dabei konstant, nur die Basis wird gerade ausgerichtet.
Höhe vs. Seitenlänge
Die Höhe ist der senkrechte Abstand zwischen parallelen Seiten, nicht die Länge einer schrägen Seite. Dies ist ein häufiger Stolperstein für Lernende.
Sinus-Alternative
Die Alternative A = a × b × sin(α) zeigt den Zusammenhang zur Vektorgeometrie. Der Sinus-Faktor "korrigiert" die Schräge zur tatsächlichen Höhe.
Invarianz unter Scherung
Die Fläche bleibt unverändert, egal wie stark das Parallelogramm "geschert" wird - solange Basis und Höhe konstant bleiben.
Anwendungen in Wissenschaft und Technik
Parallelogramme sind fundamental in vielen Bereichen:
- Mechanik: Kräfteparallelogramm zur Vektoraddition
- Maschinenbau: Parallelogrammlenker für geradlinige Führung
- Kristallographie: Einheitszellen in Kristallgittern
- Computer Graphics: Affine Transformationen und Scherungen
- Architektur: Strukturelle Elemente und Lastverteilung
- Navigation: Koordinatensysteme und Projektionen
Spezielle Parallelogramme und Verwandtschaft
Das Parallelogramm ist die Oberklasse verschiedener spezieller Vierecke:
Rechteck
Parallelogramm mit vier rechten Winkeln. Hier sind Höhe und Seitenlänge identisch, was die Flächenberechnung vereinfacht.
Rhombus (Raute)
Parallelogramm mit vier gleichen Seiten. Flächenberechnung erfolgt oft über die Diagonalen: A = (d₁ × d₂)/2.
Quadrat
Sowohl Rechteck als auch Rhombus - die "perfekte" Form mit maximaler Symmetrie und einfachster Flächenformel A = a².
Rhomboid
Allgemeiner Begriff für schiefe Parallelogramme ohne rechte Winkel oder gleiche Seiten - die "grundlegendste" Form.
Zusammenfassung
Das Parallelogramm demonstriert die Schönheit geometrischer Prinzipien: Aus einfachen Eigenschaften (parallele Seiten) entstehen elegante Beziehungen und praktische Anwendungen. Die Flächenformel A = b × h verkörpert das Prinzip der geometrischen Invarianz - die Fläche bleibt konstant unter Erhaltung von Basis und Höhe. Von der grundlegenden Vektorgeometrie bis zu komplexen ingenieurtechnischen Anwendungen bleibt das Parallelogramm ein fundamentales Werkzeug für das Verständnis unserer geometrischen Welt.
|
|