Kreisbogen berechnen

Rechner und Formeln für Kreisbogen-Berechnungen

Kreisbogen Rechner

Der Kreisbogen

Ein Kreisbogen ist ein gebogenes Kreissegment mit bestimmtem Radius und Winkel. Länge, Sehne und Winkel stehen in direkter Beziehung.

Zwei bekannte Parameter eingeben

Erster Parameter

Wählen Sie den ersten bekannten Parameter

Wert 1

Wert des ersten Parameters

Zweiter Parameter

Wählen Sie den zweiten bekannten Parameter

Wert 2

Wert des zweiten Parameters

Dezimalstellen

Kreisbogen-Eigenschaften

Kreissegment: Teil eines Kreises zwischen zwei Radien

Radius r Winkel α Bogenlänge l Sehne c

Kreisbogen-Berechnungsergebnisse

Winkel α:

Radius r:

Sehne c:

Kreisbogen l:

Kreisbogen-Struktur

Ein Kreisbogen verbindet Radius, Winkel, Bogenlänge und Sehne.
Die Bogenlänge ist proportional zum Zentriwinkel.

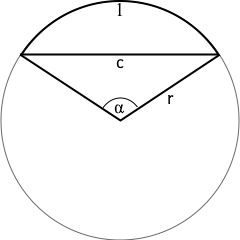
Was ist ein Kreisbogen?

Ein Kreisbogen ist ein fundamentales Element der Kreisgeometrie:

Definition: Teil der Kreislinie zwischen zwei Punkten
Zentriwinkel: Winkel α zwischen den beiden Radien
Bogenlänge: Länge l des gekrümmten Segments

Sehne: Gerade Verbindung zwischen den Endpunkten
Kreissektor: Der vom Bogen eingeschlossene Bereich
Proportionalität: Bogen proportional zum Winkel

Geometrische Eigenschaften des Kreisbogens

Der Kreisbogen weist charakteristische geometrische Beziehungen auf:

Grundparameter

Radius r: Abstand vom Mittelpunkt zu jedem Bogenpunkt
Zentriwinkel α: Winkel zwischen den Begrenzungsradien
Bogenlänge l: Länge entlang der Kreislinie
Sehne c: Direkte Verbindung der Endpunkte

Besondere Beziehungen

Proportionalität: Bogenlänge ∝ Zentriwinkel
Verhältnis zum Vollkreis: l/2πr = α/360°
Sehnen-Beziehung: Sehne kürzer als Bogenlänge
Symmetrie: Bogen symmetrisch zur Winkelhalbierenden

Mathematische Beziehungen

Der Kreisbogen folgt präzisen mathematischen Gesetzen:

Bogenlänge

l = 2πr · α/360°

Die Bogenlänge ist proportional zum Zentriwinkel. Anteil am Vollkreis entspricht Anteil am 360°-Winkel.

Sehne

c = 2r · sin(α/2)

Die Sehne verbindet die Bogenenenden direkt. Beziehung über Trigonometrie des halben Zentriwinkels.

Anwendungen von Kreisbogen

Kreisbogen finden vielfältige praktische Anwendungen:

Maschinenbau & Technik

Nocken und Kurvenscheiben
Getriebe und Zahnradprofile
Führungsschienen und Gleitbahnen
Hydraulische und pneumatische Systeme

Architektur & Bauwesen

Bögen, Gewölbe und Kuppeln
Treppen und Wendeltreppen
Brücken und Brückenbogen
Fenster- und Türbogen

Verkehr & Navigation

Straßenkurven und Autobahnauffahrten
Eisenbahnkurven und Weichen
Flugzeugkurven und Landeanflug
Schifffahrtsrouten und Hafeneinfahrten

Design & Kunst

Ornamente und dekorative Elemente
Möbeldesign und Rundungen
Logo-Gestaltung und Grafik
Uhren, Zifferblätter und Skalen

Formeln für den Kreisbogen

Bogenlänge l

\[l = 2\pi r \cdot \frac{\alpha}{360°} = \frac{\pi r \alpha}{180°}\]

Proportional zu Radius und Winkel

Sehne c

\[c = 2r \cdot \sin\left(\frac{\alpha}{2}\right)\]

Trigonometrische Beziehung zum halben Winkel

Zentriwinkel α

\[\alpha = \frac{360° \cdot l}{2\pi r} = 2 \cdot \arcsin\left(\frac{c}{2r}\right)\]

Aus Bogenlänge oder Sehne berechnen

Radius r

\[r = \frac{l \cdot 180°}{\pi \alpha} = \frac{c}{2 \sin(\alpha/2)}\]

Aus Bogenlänge/Winkel oder Sehne/Winkel

Kreissektor-Fläche A

\[A = \frac{\pi r^2 \alpha}{360°} = \frac{r \cdot l}{2}\]

Fläche des vom Bogen eingeschlossenen Sektors

Bogen-Sehnen-Verhältnis

\[\frac{l}{c} = \frac{\alpha/2}{\sin(\alpha/2)} \text{ für } \alpha \text{ in Radiant}\]

Verhältnis immer ≥ 1 (Bogen länger als Sehne)

Rechenbeispiel für einen Kreisbogen

Gegeben

Radius r = 15 Zentriwinkel α = 90°

Gesucht: Bogenlänge und Sehne des Viertelkreises

1. Bogenlänge berechnen

\[l = 2\pi \times 15 \times \frac{90°}{360°}\] \[l = 2\pi \times 15 \times 0.25 = 23.56\]

Viertel des Kreisumfangs

2. Sehne berechnen

\[c = 2 \times 15 \times \sin(45°)\] \[c = 30 \times 0.707 = 21.21\]

Diagonale des Quadrats mit Seitenlänge r

3. Kreissektor-Fläche

\[A = \frac{\pi \times 15^2 \times 90°}{360°}\] \[A = \frac{706.86}{4} = 176.71\]

Viertel der Kreisfläche

4. Verhältnisse prüfen

\[\frac{l}{c} = \frac{23.56}{21.21} = 1.11\] \[\frac{l}{2\pi r} = \frac{90°}{360°} = 0.25\]

Bogen ist 11% länger als Sehne

5. Vollständiger Kreisbogen

Radius r = 15.00 Winkel α = 90° Bogenlänge l = 23.56

Sehne c = 21.21 Sektor-Fläche A = 176.71 Viertelkreis!

Ein klassischer 90°-Viertelkreisbogen mit allen berechneten Eigenschaften

Der Kreisbogen: Grundlage gekrümmter Geometrie

Der Kreisbogen ist ein fundamentales Element der Geometrie und Ausgangspunkt für das Verständnis gekrümmter Formen. Von der antiken Architektur bis zur modernen Ingenieurstechnik bildet er die Grundlage für unzählige Konstruktionen und mathematische Konzepte.

Definition und grundlegende Eigenschaften

Der Kreisbogen verbindet elementare Geometrie mit fortgeschrittener Mathematik:

Geometrische Definition: Teil der Kreislinie zwischen zwei Punkten, definiert durch Radius und Zentriwinkel
Parametrische Darstellung: Vollständig beschreibbar durch drei Parameter: Radius, Startwinkel und Zentriwinkel
Intrinsische Krümmung: Konstante Krümmung κ = 1/r macht den Kreisbogen zur einfachsten gekrümmten Linie
Proportionalitätsprinzip: Bogenlänge ist direkt proportional zum Zentriwinkel (bei konstantem Radius)
Universelle Skalierung: Alle geometrischen Beziehungen bleiben bei Vergrößerung/Verkleinerung erhalten

Trigonometrische Beziehungen und Analysis

Der Kreisbogen ist eng mit der Trigonometrie verknüpft:

Sinus und Kosinus

Die Sehne eines Kreisbogens steht in direkter Beziehung zum Sinus des halben Zentriwinkels. Diese Verbindung macht den Kreisbogen zum geometrischen Ursprung der trigonometrischen Funktionen.

Bogenmaß (Radiant)

Das Bogenmaß definiert Winkel über das Verhältnis Bogenlänge/Radius. Ein Vollkreis entspricht 2π Radiant, was die natürliche Einheit für Winkel in der Analysis darstellt.

Grenzwertbetrachtungen

Für kleine Winkel nähert sich die Bogenlänge der Sehne an: lim(α→0) l/c = 1. Diese Grenzwertbeziehung ist fundamental für die Differentialrechnung gekrümmter Funktionen.

Reihenentwicklung

Trigonometrische Funktionen lassen sich als Potenzreihen darstellen, deren geometrische Interpretation über Kreisbogen erfolgt - eine Brücke zwischen Geometrie und Analysis.

Historische Bedeutung und Entwicklung

Der Kreisbogen hat eine reiche mathematische Geschichte:

Antike Mathematik

Bereits die alten Griechen erkannten die Bedeutung von Kreisbogen für Architektur und Astronomie. Hippokrates von Chios studierte die Quadratur von Kreisbogen-Figuren (Möndchen).

Mittelalterliche Entwicklung

Islamische Mathematiker wie Al-Battani verfeinerten die Berechnung von Kreisbogen für astronomische Zwecke und legten Grundlagen für die spätere Trigonometrie.

Renaissance und Barock

Die systematische Untersuchung von Kurven und ihren Bögen durch Descartes, Fermat und Newton führte zur analytischen Geometrie und Infinitesimalrechnung.

Moderne Mathematik

Heute sind Kreisbogen fundamental für Differentialgeometrie, komplexe Analysis und numerische Mathematik - von der Computergrafik bis zur theoretischen Physik.

Technische Anwendungen und Ingenieurswesen

Kreisbogen sind unverzichtbar in der modernen Technik:

Maschinenbau: Nocken, Kurven und Führungsbahnen nutzen Kreisbogen für präzise, vorhersagbare Bewegungsabläufe
Verkehrstechnik: Straßen- und Eisenbahnkurven folgen Kreisbogen für optimale Fahrdynamik und Sicherheit
Architektur: Bögen und Gewölbe nutzen die strukturellen Eigenschaften von Kreisbogen für Stabilität und Ästhetik
Computergrafik: Kreisbogen sind Grundelemente für Spline-Kurven und Vektorzeichnungen
Robotik: Bewegungsplanung verwendet Kreisbogen für sanfte, natürliche Roboterbewegungen
Optik: Sphärische Linsen und Spiegel basieren auf Kreisbogen-Geometrie