Kreisringsektor berechnen
Rechner und Formeln für Kreisringsektor-Berechnungen (Annulus Sector)
Kreisringsektor Rechner
Der Kreisringsektor
Ein Kreisringsektor ist ein Ausschnitt eines Kreisrings, begrenzt durch zwei Radien und einen Winkel. Kombination von Kreisring und Kreissektor.
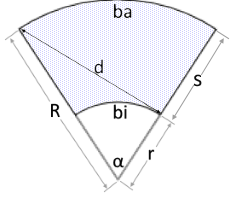
Kreisringsektor-Struktur
Ein Kreisringsektor kombiniert Ring- und Sektorgeometrie.
Begrenzt durch zwei Radien, einen Winkel und zwei Kreisbogen.
Was ist ein Kreisringsektor?
Ein Kreisringsektor ist eine komplexe geometrische Form mit mehreren Begrenzungen:
- Definition: Ausschnitt eines Kreisrings mit Winkelbegrenzung
- Doppelte Struktur: Kombination von Ring und Sektor
- Vier Begrenzungen: Zwei Radien, zwei Kreisbogen
- Drei Parameter: Äußerer Radius R, innerer Radius r, Winkel α
- Komplexe Geometrie: Vielfältige Berechnungsformeln
- Praktische Form: Häufig in Technik und Architektur
Geometrische Eigenschaften des Kreisringsektors
Der Kreisringsektor vereint Eigenschaften von Ring und Sektor:
Grundparameter
- Äußerer Radius R: Begrenzt den Sektor nach außen
- Innerer Radius r: Begrenzt den Sektor nach innen (r < R)
- Zentriwinkel α: Winkelbegrenzung des Sektors
- Seitenlänge s: s = R - r (radiale Ausdehnung)
Besondere Eigenschaften
- Zwei Kreisbogen: Äußerer Bogen ba und innerer Bogen bi
- Zwei gerade Seiten: Radiale Begrenzungslinien
- Proportionalität: Fläche proportional zu α, R² - r²
- Diagonale: Verbindung gegenüberliegender Eckpunkte
Mathematische Beziehungen
Der Kreisringsektor folgt komplexen mathematischen Gesetzen:
Flächenberechnung
Anteil des Kreisrings entsprechend dem Winkel. Kombination von Ring- und Sektorformel.
Umfangsberechnung
Summe aus beiden Kreisbogen plus beide radialen Seiten.
Anwendungen von Kreisringsektoren
Kreisringsektoren finden spezialisierte praktische Anwendungen:
Maschinenbau & Technik
- Keilriemenscheiben und Kupplungen
- Bremsscheiben und Kupplungslamellen
- Nockenscheiben und Kurvenscheiben
- Getriebe- und Motorenkomponenten
Architektur & Bauwesen
- Gewölbe- und Kuppelabschnitte
- Treppen und Wendeltreppen
- Fenster- und Türbogen
- Amphitheater und Stadionabschnitte
Datenvisualisierung
- Donut-Charts und Ringdiagramme
- Gauges und Messinstrumente
- Uhren und Zeitanzeigen
- Fortschrittsanzeigen (Progress Rings)
Design & Kunst
- Logos und grafische Elemente
- Ornamente und Verzierungen
- Keramik und Glaskunst
- Schmuck und Dekorationen
Formeln für den Kreisringsektor
Flächeninhalt A
Anteil der Ringfläche entsprechend dem Zentriwinkel
Umfang P
Beide Kreisbogen plus beide radiale Seiten
Seitenlänge s
Radiale Ausdehnung des Sektors
Äußerer Bogen ba
Kreisbogen des äußeren Radius
Innerer Bogen bi
Kreisbogen des inneren Radius
Diagonale d
Kosinussatz für das Dreieck zwischen den Radien
Rechenbeispiel für einen Kreisringsektor
Gegeben
Gesucht: Alle Eigenschaften des Kreisringsektors
1. Grundberechnungen
Seitenlänge und Winkelfaktor
2. Flächenberechnung
Ein Drittel der Ringfläche
3. Kreisbogen berechnen
Äußerer und innerer Kreisbogen
4. Umfang und Diagonale
Gesamtumfang und Diagonale
5. Vollständiger Kreisringsektor
Ein 120°-Kreisringsektor - ein Drittel des Vollrings
Der Kreisringsektor: Komplexe Geometrie vereinfacht
Der Kreisringsektor ist eine der vielseitigsten geometrischen Formen, die Ring- und Sektorgeometrie elegant verbindet. Als Ausschnitt eines Kreisrings mit Winkelbegrenzung findet er Anwendung in zahlreichen technischen und gestalterischen Bereichen, von Maschinenkomponenten bis zu modernen Datenvisualisierungen.
Definition und strukturelle Komplexität
Der Kreisringsektor vereint die Eigenschaften zweier fundamentaler geometrischer Objekte:
- Ring-Eigenschaften: Konzentrische Kreise mit äußerem Radius R und innerem Radius r
- Sektor-Eigenschaften: Winkelbegrenzung durch Zentriwinkel α und zwei radiale Geraden
- Vier Begrenzungslinien: Zwei Kreisbogen (äußerer und innerer) plus zwei gerade Radien
- Drei Parameter: Vollständig durch R, r und α charakterisiert
- Doppelte Symmetrie: Spiegelsymmetrie bezüglich der Winkelhalbierenden
Mathematische Herausforderungen und Lösungen
Die mathematische Behandlung von Kreisringsektoren erfordert die Kombination verschiedener Ansätze:
Flächenintegration
Die Fläche kann sowohl als Differenz von Kreissektoren als auch durch Polarkoordinaten-Integration berechnet werden: A = ∫∫ r dr dφ mit geeigneten Grenzen.
Umfangskomplexität
Der Umfang setzt sich aus vier verschiedenen Komponenten zusammen: zwei Kreisbogen unterschiedlicher Radien und zwei gerade Strecken radialer Richtung.
Diagonalenberechnung
Die Diagonale erfordert den Kosinussatz: d = √(R² + r² - 2Rr·cos(α)). Diese Formel verbindet alle drei Parameter elegant in einer einzigen Beziehung.
Grenzwertbetrachtungen
Für r → 0 wird der Sektor zu einem einfachen Kreissektor, für α → 360° zu einem Vollring - wichtige Spezialfälle für die Verifikation.
Technische Anwendungen und Designprinzipien
Kreisringsektoren sind essentiell in der modernen Technik und Gestaltung:
Maschinenbau-Anwendungen
Bremsscheiben, Kupplungslamellen und Keilriemenscheiben nutzen Kreisringsektor-Geometrie für optimale Kraftübertragung und Wärmeableitung. Die Form ermöglicht große Kontaktflächen bei kompakter Bauweise.
Architektonische Elemente
Gewölbesegmente, Treppen und Amphitheater-Abschnitte folgen Kreisringsektor-Geometrie. Die Form verbindet strukturelle Stabilität mit ästhetischer Eleganz.
Moderne Datenvisualisierung
Donut-Charts, Gauges und Progress-Rings nutzen Kreisringsektoren für intuitive Datendarstellung. Die Form ermöglicht mehrschichtige Informationsvermittlung auf kompaktem Raum.
Optik und Elektronik
Sektorblenden in Kameras und segmentierte Displays verwenden präzise Kreisringsektor-Geometrie für funktionale und ästhetische Zwecke.
Optimierungsprobleme und mathematische Anwendungen
Kreisringsektoren bieten interessante Optimierungsmöglichkeiten:
- Materialoptimierung: Bei gegebener Fläche minimaler Umfang oder bei gegebenem Umfang maximale Fläche
- Strukturmechanik: Optimale R/r-Verhältnisse für minimale Spannungskonzentrationen
- Fertigungsaspekte: Winkelbereiche, die effiziente Herstellungsverfahren ermöglichen
- Funktionsintegration: Kombination mehrerer Kreisringsektoren für komplexe technische Funktionen
- Ästhetische Proportionen: Goldener Schnitt und andere harmonische Verhältnisse in der Gestaltung
Verwandte geometrische Konzepte
Der Kreisringsektor steht in Beziehung zu anderen mathematischen Objekten:
Elliptische Sektoren
Verallgemeinerung zu elliptischen Ringen und deren Sektoren führt zu komplexerer Mathematik, aber auch zu vielseitigeren Anwendungen in der Technik.
3D-Erweiterungen
Kugelsektoren und Torusabschnitte erweitern das Konzept in den dreidimensionalen Raum - wichtig für Architektur und Maschinenbau.
Komplexe Analysis
Kreisringsektoren entsprechen speziellen Gebieten in der komplexen Ebene, was sie für die Funktionentheorie und conforme Abbildungen interessant macht.
Numerische Methoden
Die Diskretisierung von Kreisringsektoren ist fundamental für Finite-Elemente-Methoden und Computergrafik-Algorithmen.
Zusammenfassung
Der Kreisringsektor demonstriert eindrucksvoll, wie die Kombination einfacher geometrischer Konzepte zu einer reichen, vielseitigen Form führt. Seine mathematische Eleganz - charakterisiert durch nur drei Parameter - verbirgt eine komplexe Struktur mit vierfacher Begrenzung und vielfältigen Berechnungsformeln. Von klassischen Maschinenbauanwendungen bis zu modernen Interface-Designs zeigt der Kreisringsektor seine zeitlose Relevanz. Die Herausforderung seiner mathematischen Behandlung - von Flächenintegration bis zu Optimierungsproblemen - macht ihn zu einem idealen Objekt für das Verständnis fortgeschrittener geometrischer Konzepte. In einer zunehmend digitalisierten Welt, in der Datenvisualisierung und benutzerfreundliche Interfaces immer wichtiger werden, bleibt der Kreisringsektor ein fundamentales Werkzeug für Designer, Ingenieure und Mathematiker.