Kreissektor berechnen
Rechner und Formeln für Kreissektor-Berechnungen (Circular Sector)
Kreissektor Rechner
Der Kreissektor
Ein Kreissektor ist ein kuchenförmiger Ausschnitt eines Kreises, begrenzt durch zwei Radien und einen Kreisbogen. Auch "Tortenstück" genannt.
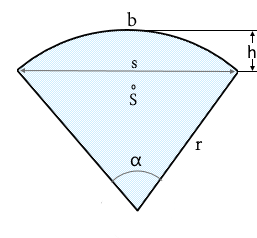
Kreissektor-Struktur
Ein Kreissektor ist wie ein Tortenstück.
Begrenzt durch zwei Radien und einen Kreisbogen.
|
|
Was ist ein Kreissektor?
Ein Kreissektor ist eine der grundlegendsten Formen der Kreisgeometrie:
- Definition: Kuchenförmiger Ausschnitt eines Kreises
- Drei Begrenzungen: Zwei Radien plus ein Kreisbogen
- Zentriwinkel: Winkel α zwischen den beiden Radien
- Proportionalität: Alle Eigenschaften proportional zu α
- Vielseitige Form: Von spitzem Keil bis fast Vollkreis
- Praktische Bedeutung: Basis für Diagramme und Messgeräte
Geometrische Eigenschaften des Kreissektors
Der Kreissektor besitzt charakteristische geometrische Eigenschaften:
Grundparameter
- Radius r: Abstand vom Mittelpunkt zur Kreislinie
- Zentriwinkel α: Winkel zwischen den Begrenzungsradien
- Kreisbogen: Gekrümmte Begrenzung des Sektors
- Sehne: Gerade Verbindung der Bogenenedpunkte
Besondere Eigenschaften
- Proportionalität: Fläche und Bogen ∝ Zentriwinkel
- Schwerpunkt: Liegt auf der Winkelhalbierenden
- Höhe: Abstand vom Mittelpunkt zur Sehne
- Symmetrie: Spiegelsymmetrie zur Winkelhalbierenden
Mathematische Beziehungen
Der Kreissektor folgt eleganten mathematischen Gesetzen:
Flächenberechnung
Die Sektorfläche ist proportional zum Zentriwinkel. Anteil der Kreisfläche entspricht Anteil des Winkels.
Bogenlänge
Der Kreisbogen ist proportional zum Radius und Winkel. Im Bogenmaß vereinfacht sich die Formel zu b = rα.
Anwendungen von Kreissektoren
Kreissektoren sind vielseitig einsetzbar:
Datenvisualisierung
- Tortendiagramme und Kuchendiagramme
- Dashboards und Kennzahlen-Displays
- Fortschrittsanzeigen (Progress Wheels)
- Gauges und Messinstrumente
Technik & Maschinenbau
- Ventile und Klappen
- Drehschalter und Potentiometer
- Turbinenschaufeln und Propeller
- Zahnradsegmente und Kupplungen
Architektur & Design
- Fensterformen und Treppenhaus-Designs
- Kuppelabschnitte und Gewölbe
- Amphitheater und Stadionabschnitte
- Garten- und Landschaftsarchitektur
Kunst & Grafik
- Logo-Design und Corporate Identity
- Ornamente und dekorative Elemente
- User Interface Design
- Keramik und Glaskunst
Formeln für den Kreissektor
Flächeninhalt A
Anteil der Kreisfläche entsprechend dem Zentriwinkel
Bogenlänge b
Kreisbogenlänge proportional zu Radius und Winkel
Umfang P
Zwei Radien plus Kreisbogen
Sehne s
Trigonometrische Beziehung zum halben Zentriwinkel
Schwerpunkt S
Abstand des Schwerpunkts vom Mittelpunkt
Höhe h
Abstand vom Mittelpunkt zur Sehne
Zentriwinkel α (aus Fläche)
Rückrechnung des Winkels aus der Fläche
Zentriwinkel α (aus Sehne)
Rückrechnung des Winkels aus der Sehne
Rechenbeispiel für einen Kreissektor
Gegeben
Gesucht: Alle Eigenschaften des 60°-Sektors (Sechstel des Kreises)
1. Fläche und Bogenlänge
Ein Sechstel der Kreisfläche und des Umfangs
2. Sehne und Umfang
Bei 60° ist die Sehne gleich dem Radius!
3. Schwerpunkt und Höhe
Schwerpunkt und Abstand zur Sehne
4. Besondere 60°-Eigenschaften
Der 60°-Sektor bildet ein gleichseitiges Dreieck
5. Vollständiger 60°-Kreissektor
Ein besonderer Sektor - bildet zusammen mit dem Mittelpunkt ein gleichseitiges Dreieck
Der Kreissektor: Grundbaustein der Kreisgeometrie
Der Kreissektor ist eine der fundamentalsten und vielseitigsten geometrischen Formen. Als "Tortenstück" des Kreises verbindet er elementare Geometrie mit praktischen Anwendungen und ist aus der modernen Datenvisualisierung, dem Maschinenbau und der Architektur nicht wegzudenken.
Definition und geometrische Struktur
Der Kreissektor zeichnet sich durch seine elegante Einfachheit aus:
- Dreifache Begrenzung: Zwei Radien vom Mittelpunkt plus ein Kreisbogen
- Winkelabhängigkeit: Alle Eigenschaften direkt proportional zum Zentriwinkel α
- Skalierbarkeit: Form bleibt bei Vergrößerung/Verkleinerung erhalten
- Symmetrie: Spiegelsymmetrie bezüglich der Winkelhalbierenden
- Kontinuierlicher Übergang: Von infinitesimal kleinem Keil bis fast Vollkreis
Mathematische Eleganz und Proportionalität
Die Mathematik des Kreissektors besticht durch ihre Klarheit:
Proportionalitätsprinzip
Alle wichtigen Eigenschaften (Fläche, Bogenlänge) sind direkt proportional zum Zentriwinkel. Dies macht Berechnungen intuitiv und vorhersagbar.
Trigonometrische Verbindungen
Die Sehnenformel s = 2r·sin(α/2) verbindet den Sektor elegant mit der Trigonometrie und zeigt die fundamentale Rolle des Sinus.
Schwerpunktberechnung
Der Schwerpunkt liegt stets auf der Winkelhalbierenden in einem Abstand von 2r·sin(α/2)/(3·α) vom Mittelpunkt - eine bemerkenswerte geometrische Konstante.
Grenzwertverhalten
Für kleine Winkel nähert sich der Sektor einem Dreieck, für große Winkel dem Vollkreis - wichtig für Näherungsrechnungen.
Moderne Anwendungen und Datenvisualisierung
In der digitalen Ära hat der Kreissektor eine Renaissance erlebt:
Datenvisualisierung
Kreisdiagramme (Pie Charts) nutzen Sektoren für intuitive Darstellung von Anteilen. Die Winkel entsprechen direkt den Datenwerten - eine natürliche Proportionsdarstellung.
Interactive Interfaces
Moderne Benutzeroberflächen verwenden Kreissektoren für Fortschrittsanzeigen, Menüs und Steuerelemente - von Smartphone-Apps bis zu industriellen Dashboards.
Messinstrumente
Analoge und digitale Messgeräte (Tachometer, Manometer) nutzen Kreissektoren für präzise und ablesbare Wertdarstellung.
Gaming und VR
Spiele und Virtual-Reality-Anwendungen verwenden sektorbasierte Interfaces für natürliche, kreisförmige Menüführung und Statusanzeigen.
Technische und architektonische Anwendungen
Kreissektoren sind essentiell in der praktischen Anwendung:
- Maschinenbau: Ventile, Klappen und Drehschalter nutzen Sektorgeometrie für präzise Öffnungswinkel
- Turbinentechnik: Schaufeln und Rotoren folgen Sektorprinzipien für optimale Strömungsführung
- Architektur: Kuppeln, Treppen und Amphitheater verwenden Sektorabschnitte für strukturelle und ästhetische Zwecke
- Optik: Segmentierte Spiegel und Linsen in Teleskopen basieren auf Sektorgeometrie
- Elektronik: Drehkondensatoren und Potentiometer nutzen variable Sektorüberlappung
Besondere Winkel und ihre Eigenschaften
Bestimmte Winkel ergeben besonders elegante Eigenschaften:
60° (π/3) - Der harmonische Sektor
Bei 60° ist die Sehne gleich dem Radius, was ein gleichseitiges Dreieck bildet. Diese Eigenschaft macht ihn ideal für konstruktive Anwendungen.
90° (π/2) - Der Viertelkreis
Der rechtwinklige Sektor ist fundamental für Koordinatensysteme und technische Konstruktionen. Seine Sehne entspricht r√2.
180° (π) - Der Halbkreis
Der größtmögliche echte Sektor wird zum Halbkreis mit gerader Sehne als Durchmesser. Fundamental für viele geometrische Konstruktionen.
120° (2π/3) - Der Drittelkreis
Drei solche Sektoren bilden einen Vollkreis - wichtig für symmetrische Designs und technische Anwendungen mit dreifacher Teilung.
Zusammenfassung
Der Kreissektor verkörpert geometrische Eleganz in Reinform. Seine einfache Definition - ein Ausschnitt zwischen zwei Radien - verbirgt eine reiche mathematische Struktur mit direkten Proportionalitäten und eleganten trigonometrischen Beziehungen. Von antiken astronomischen Berechnungen bis zu modernen Datenvisualisierungen bleibt der Kreissektor ein fundamentales Werkzeug für die intuitive Darstellung von Anteilen und Winkeln. Seine Vielseitigkeit - von winzigen Interface-Elementen bis zu monumentalen Architekturformen - demonstriert die zeitlose Relevanz grundlegender geometrischer Prinzipien. In einer zunehmend datengetriebenen Welt, in der visuelle Kommunikation immer wichtiger wird, bleibt der Kreissektor ein unverzichtbares Element für Designer, Ingenieure und Mathematiker.