Kreissegment berechnen
Rechner und Formeln für Kreissegment-Berechnungen (Kreisabschnitt)
Kreissegment Rechner
Das Kreissegment
Ein Kreissegment ist ein Kreisabschnitt, der durch eine Sehne vom Kreis getrennt wird. Auch "Kreiskappe" oder "Kreisabschnitt" genannt.
Kreissegment-Struktur
Ein Kreissegment ist der kleinere Bereich eines geteilten Kreises.
Abgetrennt durch eine gerade Sehne vom restlichen Kreis.
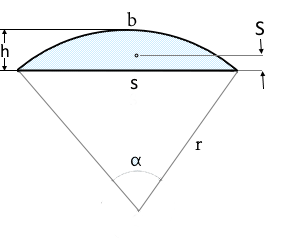
Was ist ein Kreissegment?
Ein Kreissegment ist eine fundamentale geometrische Form mit besonderen Eigenschaften:
- Definition: Kreisabschnitt, abgetrennt durch eine Sehne
- Zwei Begrenzungen: Kreisbogen und gerade Sehne
- Asymmetrische Form: Unterschied zu Kreissektor
- Höhe h: Abstand von Sehne zum äußersten Bogenpunkt
- Vielseitige Größe: Von flacher Kappe bis fast Halbkreis
- Praktische Bedeutung: Architektur, Optik, Maschinenbau
Geometrische Eigenschaften des Kreissegments
Das Kreissegment besitzt charakteristische geometrische Eigenschaften:
Grundparameter
- Radius r: Radius des ursprünglichen Kreises
- Höhe h: Abstand von Sehne zum fernsten Bogenpunkt
- Sehne s: Gerade Begrenzungslinie des Segments
- Zentriwinkel α: Winkel des zugehörigen Kreissektors
Besondere Eigenschaften
- Asymmetrie: Unterschiedlich zu radialsymmetrischen Sektoren
- Höhen-Beziehung: h = r - r·cos(α/2)
- Schwerpunkt: Liegt auf der Symmetrieachse
- Grenzfall: Bei h=r wird es zum Halbkreis
Mathematische Beziehungen
Das Kreissegment folgt komplexen mathematischen Gesetzen:
Flächenberechnung
Segment = Sektor minus Dreieck. Komplexe Beziehung zwischen Winkel und Fläche.
Höhen-Radius-Beziehung
Die Höhe hängt trigonometrisch vom halben Zentriwinkel ab.
Anwendungen von Kreissegmenten
Kreissegmente finden vielfältige praktische Anwendungen:
Architektur & Bauwesen
- Kuppelsegmente und Gewölbeabschnitte
- Brückenbogen und Tunnelprofile
- Fensterformen und Türbogen
- Dachkonstruktionen und Überdachungen
Maschinenbau & Technik
- Nocken und Kurvensteuerungen
- Behälter und Tankquerschnitte
- Ventile und Klappen
- Rotoren und Turbinenprofile
Optik & Lichttechnik
- Linsen und optische Elemente
- Reflektoren und Spiegel
- Prismen und Lichtleiter
- Beleuchtungsoptiken
Wasserbau & Hydraulik
- Kanalquerschnitte und Rohrleitungen
- Wehre und Überfallkanten
- Schleusen und Wasserbauwerke
- Strömungsoptimierung
Formeln für das Kreissegment
Flächeninhalt A
Kreissektor minus eingeschriebenes Dreieck
Höhe h
Abstand von Sehne zum äußersten Bogenpunkt
Sehne s
Gerade Begrenzungslinie des Segments
Bogenlänge b
Gekrümmte Begrenzungslinie (Winkel im Bogenmaß)
Umfang P
Sehne plus Kreisbogen
Zentriwinkel α (aus Höhe)
Rückrechnung des Winkels aus Höhe und Radius
Schwerpunkt S
Abstand des Schwerpunkts vom Kreismittelpunkt
Höhe h (aus Sehne)
Höhe berechnen wenn Sehne bekannt ist
Rechenbeispiel für ein Kreissegment
Gegeben
Gesucht: Alle Eigenschaften des Kreissegments
1. Zentriwinkel berechnen
Umrechnung von Höhe und Radius zu Winkel
2. Sehne berechnen
Sehne über trigonometrische Beziehung
3. Fläche und Bogenlänge
Fläche und Bogenlänge des Segments
4. Umfang und Schwerpunkt
Gesamtumfang und Schwerpunktabstand
5. Vollständiges Kreissegment
Ein Kreissegment mit mittlerer Höhe - typisch für Architekturanwendungen
Das Kreissegment: Asymmetrische Kreisgeometrie
Das Kreissegment ist eine der faszinierendsten Formen der Kreisgeometrie. Im Gegensatz zum radialsymmetrischen Kreissektor wird das Segment durch eine Sehne begrenzt, was zu asymmetrischen, aber dennoch eleganten mathematischen Beziehungen führt. Diese Form findet breite Anwendung in Architektur, Maschinenbau und Optik.
Definition und strukturelle Besonderheiten
Das Kreissegment unterscheidet sich fundamental von anderen Kreisformen:
- Sehnen-Begrenzung: Eine gerade Linie trennt das Segment vom restlichen Kreis
- Asymmetrische Struktur: Keine Radialsymmetrie wie beim Kreissektor
- Höhen-Parameter: Die Höhe h ist ein charakteristisches Maß für die Segmentform
- Zwei Begrenzungen: Kreisbogen und gerade Sehne bilden den Umfang
- Variabilität: Von flacher Kappe bis zu fast halbkreisförmigen Segmenten
Mathematische Komplexität und Eleganz
Die Mathematik des Kreissegments verbindet verschiedene geometrische Konzepte:
Differenz-Prinzip
Die Segmentfläche ergibt sich als Differenz zwischen Kreissektor und eingeschriebenem Dreieck: A = ½r²(α - sin α). Diese elegant einfache Formel verbirgt komplexe trigonometrische Beziehungen.
Höhen-Trigonometrie
Die Beziehung h = r(1 - cos(α/2)) verbindet die intuitive Höhe mit dem abstrakten Zentriwinkel über trigonometrische Funktionen.
Schwerpunktberechnung
Der Schwerpunkt erfordert Integration über die asymmetrische Form: S = s³/(12A) - r·cos(α/2). Diese Formel zeigt die mathematische Raffinesse der Segmentgeometrie.
Parameterumrechnung
Die Umrechnung zwischen Höhe, Sehne, Winkel und Radius erfordert inverse trigonometrische Funktionen, was das Segment mathematisch anspruchsvoller macht als andere Kreisformen.
Architektonische und ingenieurtechnische Bedeutung
Kreissegmente sind fundamental in der praktischen Anwendung:
Struktureller Vorteil
Segmentförmige Bögen und Gewölbe nutzen die natürliche Druckverteilung kreisförmiger Strukturen, während die flache Sehne praktische Vorteile für Auflagerkonstruktionen bietet.
Materialoptimierung
Die Segmentform ermöglicht optimale Material-Leistungs-Verhältnisse: maximale strukturelle Effizienz bei minimalem Materialaufwand für Überdachungen und Gewölbe.
Hydraulische Anwendungen
In der Wassertechnik ermöglichen segmentförmige Kanalquerschnitte optimale Fließeigenschaften bei verschiedenen Füllständen - ein klassisches Optimierungsproblem der Hydraulik.
Optische Systeme
Linsensegmente und asphärische Optiken nutzen die kontrollierte Krümmung von Kreissegmenten für präzise Lichtführung und Aberrationskorrektur.
Spezielle Anwendungsfälle und Optimierungsprobleme
Das Kreissegment führt zu interessanten Optimierungsproblemen:
- Tankfüllstand: Berechnung von Volumina in teilgefüllten zylindrischen Tanks
- Brückenbau: Optimale Bogenhöhe für maximale Tragfähigkeit bei gegebener Spannweite
- Solartechnik: Parabolspiegelsegmente für optimale Lichtkonzentration
- Strömungstechnik: Kanalprofile für minimalen Strömungswiderstand
- Architektur: Fensterformen für optimale Lichtausbeute bei strukturellen Beschränkungen
Berechnungsstrategien und numerische Aspekte
Die praktische Berechnung von Kreissegmenten erfordert verschiedene Ansätze:
Direkte Formeln
Wenn Radius und Winkel bekannt sind, führen die direkten trigonometrischen Formeln zu exakten Ergebnissen. Dies ist der mathematisch eleganteste Weg.
Iterative Verfahren
Bei gegebener Höhe und Sehne müssen inverse trigonometrische Funktionen numerisch berechnet werden - ein typisches Problem der Ingeneursmathematik.
Näherungsformeln
Für flache Segmente (h << r) existieren Näherungsformeln, die praktische Berechnungen vereinfachen, ohne wesentlich an Genauigkeit zu verlieren.
CAD-Integration
Moderne CAD-Systeme verwenden parametrische Darstellungen von Kreissegmenten, die automatische Neuberechnung bei Parameteränderungen ermöglichen.
Zusammenfassung
Das Kreissegment verkörpert die perfekte Balance zwischen mathematischer Komplexität und praktischer Anwendbarkeit. Seine asymmetrische Struktur - begrenzt durch Kreisbogen und Sehne - führt zu eleganten, aber anspruchsvollen mathematischen Beziehungen, die inverse trigonometrische Funktionen und Differenzberechnungen erfordern. Von der antiken Architektur bis zur modernen Ingenieurtechnik bleibt das Kreissegment eine fundamentale Form für strukturelle, hydraulische und optische Anwendungen. Seine mathematische Raffinesse - exemplifiziert durch die Schwerpunktformel oder die Höhen-Winkel-Beziehung - macht es zu einem idealen Objekt für das Verständnis fortgeschrittener geometrischer Konzepte. In einer Welt, in der Optimierung und Materialeffizienz immer wichtiger werden, bleibt das Kreissegment ein unverzichtbares Werkzeug für Ingenieure, Architekten und Mathematiker.