Kreiswinkel berechnen
Rechner und Formeln für Kreiswinkel-Berechnungen (Circular Angles)
Kreiswinkel Rechner
Kreiswinkel
Kreiswinkel sind die charakteristischen Winkel in der Kreisgeometrie: Zentriwinkel μ, Tangentenwinkel θ und deren Beziehungen.
Kreiswinkel-Struktur
Kreiswinkel zeigen fundamentale Winkelbeziehungen.
θ = μ/2 ist eine der wichtigsten Beziehungen der Kreisgeometrie.
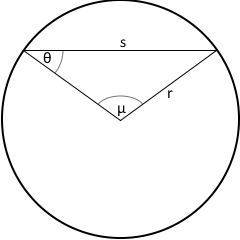
Was sind Kreiswinkel?
Kreiswinkel sind fundamentale Winkel in der Kreisgeometrie:
- Zentriwinkel μ: Winkel im Kreismittelpunkt
- Tangentenwinkel θ: Winkel zwischen Radius und Sehne
- Grundbeziehung: θ = μ/2
- Geometrische Basis: Für viele Kreisberechnungen
- Trigonometrische Verbindung: Zu Sinus und Kosinus
- Praktische Bedeutung: Navigation, Vermessung, Optik
Geometrische Eigenschaften der Kreiswinkel
Kreiswinkel folgen grundlegenden geometrischen Gesetzen:
Winkeltypen
- Zentriwinkel μ: Vom Mittelpunkt aus gemessen
- Tangentenwinkel θ: Zwischen Radius und Sehne
- Umfangswinkel: Von Kreisumfang aus gemessen
- Innenwinkel: Im Dreieck Mittelpunkt-Sehnenenden
Fundamentale Beziehungen
- Halbwinkel-Regel: θ = μ/2
- Trigonometrische Verbindung: sin(θ) = s/(2r)
- Kosinussatz-Anwendung: Sehnenberechnung
- Symmetrie: Gleichschenklige Dreiecke
Mathematische Beziehungen
Kreiswinkel bilden die Basis vieler trigonometrischer Beziehungen:
Halbwinkel-Theorem
Der Tangentenwinkel ist immer die Hälfte des Zentriwinkels. Fundamentales Gesetz der Kreisgeometrie.
Sehnen-Beziehung
Sehne über Tangentenwinkel und Radius berechnen. Direkte trigonometrische Verbindung.
Anwendungen von Kreiswinkel-Berechnungen
Kreiswinkel sind essentiell in vielen Bereichen:
Navigation & Vermessung
- GPS-Berechnungen und Triangulation
- Kompassnavigation und Peilung
- Landvermessung und Kartographie
- Astronomische Positionsbestimmung
Maschinenbau & Technik
- Zahnradgeometrie und Verzahnungen
- Kurvenscheiben und Nocken
- Roboterkinematik und Gelenkwinkel
- Präzisionsmechanik und Uhrentechnik
Optik & Lichttechnik
- Linsensysteme und Aberrationen
- Spiegelteleskope und Reflektoren
- Lasertechnik und Strahlengang
- Kameraoptik und Bildqualität
Architektur & Bauwesen
- Kuppeln und Gewölbekonstruktionen
- Brückenbogen und Tragwerke
- Sonnenstudien und Schattenwurf
- Rundbauten und Spiraltreppen
Formeln für Kreiswinkel
Tangentenwinkel θ
Fundamentale Halbwinkel-Beziehung
Zentriwinkel μ
Berechnung aus Radius und Sehne
Sehne s
Berechnung aus Radius und Zentriwinkel
Radius r
Berechnung aus Sehne und Zentriwinkel
Alternative Sehnen-Formel
Über Tangentenwinkel oder halben Zentriwinkel
Umfangswinkel-Beziehung
Umfangswinkel = Tangentenwinkel (Thales-Kreis)
Rechenbeispiel für Kreiswinkel
Gegeben
Gesucht: Zentriwinkel μ und Tangentenwinkel θ
1. Zentriwinkel berechnen
Anwendung der Kosinus-Formel
2. Tangentenwinkel berechnen
Fundamentale Halbwinkel-Beziehung
3. Verifikation über Sinus
Bestätigung durch alternative Berechnung
4. Geometrische Interpretation
\[\frac{s}{2r} = \frac{30}{50} = 0.6 = \sin(36.87°)\]
Verbindung zu bekannten Dreiecks-Verhältnissen
5. Vollständige Kreiswinkel-Lösung
Ein klassisches 3-4-5 Dreieck-Verhältnis in Kreiswinkel-Darstellung
Kreiswinkel: Fundamentale Geometrie und Trigonometrie
Kreiswinkel bilden das Herzstück der Kreisgeometrie und sind fundamental für das Verständnis trigonometrischer Beziehungen. Die elegante Beziehung θ = μ/2 zwischen Tangentenwinkel und Zentriwinkel ist eine der schönsten und praktischsten Gesetzmäßigkeiten der Geometrie.
Historische Entwicklung und mathematische Bedeutung
Die Theorie der Kreiswinkel hat eine reiche mathematische Geschichte:
- Antike Grundlagen: Thales und Euklid erkannten bereits fundamentale Winkelbeziehungen
- Mittelalterliche Entwicklung: Islamische Mathematiker verfeinerten trigonometrische Anwendungen
- Renaissance-Fortschritte: Präzise Winkelmessungen für Navigation und Astronomie
- Moderne Anwendungen: Von GPS-Systemen bis zu Robotersteuerungen
- Theoretische Basis: Grundlage für komplexe Zahlen und Fourier-Analysis
Fundamentale Winkelbeziehungen
Die Kreiswinkel-Theorie basiert auf eleganten mathematischen Prinzipien:
Halbwinkel-Theorem
Die Beziehung θ = μ/2 ist nicht nur eine praktische Formel, sondern Ausdruck der fundamentalen Symmetrie des Kreises. Sie verbindet zentrale und periphere Winkelmessung elegant.
Trigonometrische Verbindung
Kreiswinkel bilden die geometrische Grundlage für Sinus, Kosinus und Tangens. Die Einheitskreis-Definition der trigonometrischen Funktionen basiert direkt auf Kreiswinkeln.
Umfangswinkel-Satz
Alle Umfangswinkel über demselben Kreisbogen sind gleich - ein fundamentaler Satz, der direkt aus der Kreiswinkel-Theorie folgt und unzählige Anwendungen ermöglicht.
Komplexe Zahlen
In der komplexen Ebene entsprechen Kreiswinkel Rotationen, was sie fundamental für Fourier-Transformationen und Signalverarbeitung macht.
Praktische Anwendungen in Wissenschaft und Technik
Kreiswinkel sind essentiell in zahlreichen technischen Bereichen:
Navigation und GPS
GPS-Berechnungen basieren auf sphärischer Trigonometrie, die direkt aus Kreiswinkel-Prinzipien entwickelt wurde. Satellitenpositionierung verwendet kontinuierlich Winkelberechnungen.
Robotik und Automatisierung
Robotergelenke und Bewegungssteuerung verwenden Kreiswinkel für präzise Positionierung und Pfadplanung. Inverse Kinematik ist ohne Winkelberechnungen undenkbar.
Optik und Lasertechnik
Linsensysteme, Strahlengang und Aberrationskorrektur nutzen Kreiswinkel-Berechnungen für präzise optische Designs. Jede Kamera und jedes Teleskop basiert darauf.
Maschinenbau und Konstruktion
Zahnradgeometrie, Kurvenscheiben und Präzisionsmechanik erfordern exakte Winkelberechnungen. Ohne Kreiswinkel-Theorie wäre moderne Maschinentechnik unmöglich.
Berechnungsstrategien und numerische Aspekte
Die praktische Berechnung von Kreiswinkeln erfordert verschiedene Ansätze:
- Direkte Formeln: Wenn Grundparameter bekannt sind, führen trigonometrische Formeln zu exakten Ergebnissen
- Inverse Trigonometrie: arcsin, arccos, arctan für Rückberechnungen - numerisch anspruchsvoll
- Iterative Verfahren: Für komplexe Systeme mit mehreren Unbekannten
- CAD-Integration: Automatische Winkelberechnung in modernen Konstruktionsprogrammen
- Präzisionsanforderungen: Astronomie und GPS erfordern Genauigkeit bis zur Mikrobogensekunde
Erweiterte mathematische Verbindungen
Kreiswinkel verbinden verschiedene mathematische Gebiete:
Analytische Geometrie
Kreisgleichungen und Parameterdarstellungen basieren auf Winkel-Koordinaten. Rotation und Transformation nutzen Winkel als natürliche Parameter.
Differentialgeometrie
Krümmung und Torsion von Kurven werden über Winkeländerungen definiert. Kreiswinkel sind Grundlage für die Theorie gekrümmter Räume.
Schwingungslehre
Harmonische Schwingungen sind direkt mit Kreisbewegungen verknüpft. Phasenwinkel und Frequenzanalyse basieren auf Kreiswinkel-Konzepten.
Quantenmechanik
Quantenphasen und Wahrscheinlichkeitsamplituden verwenden komplexe Winkelfunktionen, die aus klassischen Kreiswinkeln entwickelt wurden.
Zusammenfassung
Kreiswinkel repräsentieren eine der elegantesten Verbindungen zwischen elementarer Geometrie und höherer Mathematik. Die fundamentale Beziehung θ = μ/2 ist nicht nur eine praktische Berechnungsformel, sondern Ausdruck tiefliegender geometrischer Symmetrien. Von der antiken Astronomie bis zur modernen Robotik, von der GPS-Navigation bis zur Quantenphysik - Kreiswinkel bilden eine unverzichtbare mathematische Grundlage. Ihre Bedeutung reicht weit über die reine Geometrie hinaus und macht sie zu einem zentralen Werkzeug für Ingenieure, Physiker und Mathematiker. In einer zunehmend technisierten Welt, in der Präzision und Automation immer wichtiger werden, bleiben Kreiswinkel ein fundamentales und zeitloses mathematisches Konzept.