Calculate Triangle Area
Calculate the area of a triangle from two sides and an angle
Triangle Area Calculator
Area Calculation with Sine
The triangle area is calculated from two sides and the included angle.
Visualization
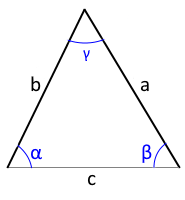
The diagram shows a triangle with two sides and the included angle.
The area is calculated with the sine formula.
Angle Assignment:
For sides a, b enter angle γ.
For sides b, c enter angle α.
For sides a, c enter angle β.
What is Triangle Area?
The triangle area is the area of the region enclosed by three sides:
- Basic formula: A = ½ × base × height
- Sine formula: A = ½ × a × b × sin(γ)
- Included angle: The angle between the two given sides
- Unit: Square units (m², cm², etc.)
- Applications: Construction planning, geometry, surveying
- Advantage: Simple calculation from two sides and angle
The Sine Formula for Triangle Areas
The sine formula enables area calculation from two sides and the included angle:
Mathematical Background
- Based on the trigonometric sine function
- Uses the relationship between angle and height
- Height h = b × sin(γ) with base a
- This gives: A = ½ × a × b × sin(γ)
Practical Advantages
- No height measurement required
- Direct calculation from available data
- Works for all triangle types
- Particularly useful in surveying
Different Calculation Methods
There are different formulas for area calculation, depending on given parameters:
Base × Height
Classic formula with known height
Sine Formula
For two sides and included angle
Heron's Formula
For three known sides
Formulas for Triangle Area Calculation
Sine Formulas for Different Side Combinations
Sides a, b with angle γ
Sides a, c with angle β
Sides b, c with angle α
Basic Formula
Base times height divided by 2
Vector Formula
Cross product of two vectors
Heron's Formula
s = (a+b+c)/2 (semi-perimeter)
Coordinate Formula
For triangles in coordinate system
Symbols and Notation
- A: Area of the triangle
- a, b, c: Side lengths of the triangle
- α, β, γ: Interior angles of the triangle
- h: Height of the triangle
- g: Base of the triangle
- s: Semi-perimeter (a+b+c)/2
- sin: Sine function
- °: Degrees (angle measure)
Calculation Example
Given
Apply Sine Formula
Substitute the given values
Calculation
The area is approximately 8.66 square units
Verification
- Plausibility: Area is positive
- Magnitude: Fits with side lengths
- Special case: At 90° would be A = 10
Applications
Land surveying, construction planning, CAD software, material calculation.
Triangle Area Calculation in Theory and Practice
The area calculation of triangles is one of the most fundamental problems in geometry and has far-reaching applications in mathematics, physics, engineering and many other fields. The sine formula is particularly elegant and practical.
The Sine Formula: Mathematical Background
The sine formula A = ½ab sin(γ) is based on the fundamental relationship between angles and side ratios in triangles:
- Trigonometric foundation: The height h to side a equals h = b × sin(γ)
- Area formula: A = ½ × base × height = ½ × a × h = ½ × a × b × sin(γ)
- Universality: The formula works for all triangle types
- Symmetry: Analogous formulas exist for all three side combinations
Different Calculation Methods
Classical Methods
- Base × Height: A = ½gh (with known height)
- Heron's formula: A = √[s(s-a)(s-b)(s-c)] (three sides)
- Sine formula: A = ½ab sin(γ) (two sides, one angle)
Modern Approaches
- Coordinate geometry: Determinant formula
- Vector algebra: Cross product |a⃗ × b⃗|/2
- Complex numbers: Imaginary part formula
Practical Applications
Triangle area calculation is found in countless practical areas:
- Surveying: Property areas, triangulation, GPS calculations
- Construction: Roof areas, structural elements, material calculation
- Computer graphics: 3D rendering, polygon meshes, area calculation
- Physics: Force diagrams, center of gravity calculations, moment analysis
- Navigation: Bearing, course calculations, position determination
- Agriculture: Field sizes, irrigation planning, yield estimation
Advantages of the Sine Formula
Practical Advantages
- No height measurement required
- Directly calculable from available data
- Works for all triangle types
- Particularly precise with known side lengths
Mathematical Elegance
- Compact, symmetric formula
- Direct trigonometric relationship
- Extendable to arbitrary polygons
- Basis for further calculations
Trigonometric Foundations
Understanding the sine function is essential for area calculation:
- Definition: sin(α) = opposite / hypotenuse in right triangle
- Range: -1 ≤ sin(α) ≤ 1 for all angles α
- Special values: sin(30°) = 0.5, sin(60°) = √3/2, sin(90°) = 1
- Symmetries: sin(180° - α) = sin(α), sin(α + 360°) = sin(α)
Error Sources and Accuracy
In practical application of the sine formula, various aspects must be considered:
- Angle units: Note distinction between degrees and radians
- Rounding errors: Use sufficient decimal places
- Measurement errors: Consider inaccuracies in side lengths and angles
- Limiting cases: Very acute or obtuse angles can cause problems
Historical Development
Triangle area calculation has a long mathematical history:
- Antiquity: Already known to Babylonians and Egyptians
- Greece: Euclid systematized area theory
- Middle Ages: Arab mathematicians developed trigonometry
- Renaissance: Precise trigonometric tables enabled accurate calculations
- Modern era: Computer algorithms for high-precision calculations
Extensions and Generalizations
The basic principles can be extended to more complex geometries:
- Polygons: Decomposition into triangles for area calculation
- 3D geometry: Surface calculations of polyhedra
- Spherical trigonometry: Triangles on sphere surfaces
- Analytic geometry: Integration for curvilinearly bounded areas
Summary
The sine formula for triangle area calculation is an elegant mathematical tool with broad practical applications. It connects basic trigonometric concepts with geometric problems and forms the basis for many advanced calculations in science and technology. Its simplicity and universality make it an indispensable component of mathematical basic education.
|
|
Bisector of a triangle • Equilateral triangle • Right triangles • Right triangle, given 1 side and 1 angle • Isosceles right triangles • Isosceles triangles • Triangle area, given 2 sides and 1 anglee • Triangle area, given 1 side and 2 angles • Triangle, Incircle, given 3 sides • Area of a triangle given base and height • Triangle vertices, 3 x/y points •