Calculate Triangle in Coordinate System
Analytical geometry: Calculate triangles from vertex coordinates
Coordinate Triangle Calculator
Analytical Geometry
Calculate all properties of a triangle from the coordinates of the three vertices. Uses vector calculation and analytical methods.
Coordinate System
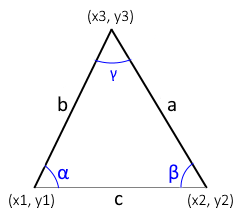
The triangle is defined by three points A, B, C in the Cartesian coordinate system.
All geometric properties are calculated analytically.
Triangle in Coordinate System
A triangle in the coordinate system is completely defined by three points:
- Point A (x₁, y₁): First vertex of the triangle
- Point B (x₂, y₂): Second vertex of the triangle
- Point C (x₃, y₃): Third vertex of the triangle
- Analytical calculation: All properties from coordinates
- Vector calculation: Side lengths and angles
- Determinants: Area calculation
Analytical Geometry Methods
Analytical geometry enables precise calculations with coordinates:
Distance Formula
- Side lengths from coordinate differences
- Application of Pythagorean theorem
- d = √[(x₂-x₁)² + (y₂-y₁)²]
- Precise calculation of all three sides
Area Formula
- Determinant-based calculation
- Shoelace formula (Gaussian trapezoid formula)
- A = ½|x₁(y₂-y₃) + x₂(y₃-y₁) + x₃(y₁-y₂)|
- Automatically considers orientation
Vector Calculation and Angles
Vectors and the dot product enable angle calculations:
Form Vectors
- Side vectors from point differences
- Vector AB = (x₂-x₁, y₂-y₁)
- Magnitude |AB| = side length
- Direction and length combined
Calculate Angles
- Dot product of two vectors
- cos(α) = (u⃗ · v⃗) / (|u⃗| |v⃗|)
- Application of law of cosines
- All three interior angles calculable
Calculation Algorithm
The calculator uses a systematic approach for the calculation:
Step 1
Calculate side lengths with distance formula
Step 2
Area with determinant formula
Step 3
Angles with law of cosines
Step 4
Perimeter as sum of sides
Formulas for Coordinate Triangles
Area A
Determinant formula (Shoelace formula)
Perimeter U
Sum of all three side lengths
Side Lengths (Distance Formula)
\[a = \sqrt{(x_2-x_3)^2 + (y_2-y_3)^2}\]
\[b = \sqrt{(x_1-x_3)^2 + (y_1-y_3)^2}\]
\[c = \sqrt{(x_1-x_2)^2 + (y_1-y_2)^2}\]
Angles (Law of Cosines)
\[\alpha = \arccos\left(\frac{b^2+c^2-a^2}{2bc}\right)\]
\[\beta = \arccos\left(\frac{a^2+c^2-b^2}{2ac}\right)\]
\[\gamma = \arccos\left(\frac{a^2+b^2-c^2}{2ab}\right)\]
Coordinates and Notation
- A(x₁, y₁): First vertex of the triangle
- B(x₂, y₂): Second vertex of the triangle
- C(x₃, y₃): Third vertex of the triangle
- a, b, c: Side lengths (opposite to the points)
- α, β, γ: Interior angles at the vertices
- A: Area of the triangle
- U: Perimeter of the triangle
- °: Degrees (angle measure)
Calculation Example
Given
1. Calculate Side Lengths
\[ c = \sqrt{(3-(-2))^2 + (3-(-1))^2 }= \sqrt{25 + 16}= \sqrt{41} ≈ 6.40 \]
Pythagorean theorem in coordinates
2. Calculate Area
Determinant formula
3. Special Features
- All coordinates: Integer values
- Orientation: Automatically considered
- Precision: Exact analytical methods
- Complete: All parameters calculable
Analytical Geometry and Coordinate Triangles
Analytical geometry (also called coordinate geometry) is a fundamental area of mathematics that solves geometric problems through algebraic methods. The calculation of triangles from coordinates of their vertices shows the elegance and power of this approach.
Fundamentals of Coordinate Geometry
The Cartesian coordinate system makes it possible to describe geometric objects algebraically:
- Point representation: Each point is uniquely determined by a coordinate pair (x, y)
- Distance measurement: The distance between points follows the Pythagorean theorem
- Angle calculation: Possible through vector calculation and dot product
- Area calculation: Elegant formulas with determinants
- Algebraic methods: Geometric problems become computational tasks
The Distance Formula
The foundation of all length measurements in the coordinate system is the distance formula:
Derivation
The formula derives directly from the Pythagorean theorem: A right triangle with legs |x₂-x₁| and |y₂-y₁| has hypotenuse d.
Application
Each side length of the triangle is calculated as the distance between two of its vertices.
Advantages
Works in all quadrants, automatically considers negative coordinates, always delivers positive distances.
Precision
Exact calculation without approximations, as long as the coordinates are exact.
Area Calculation with Determinants
The determinant formula for triangle area is a masterpiece of analytical geometry:
- Shoelace formula: Also known as Gaussian trapezoid formula
- Orientation: The absolute value ensures the area is always positive
- Efficiency: Direct calculation without detour through side lengths and heights
- Generalization: Works for arbitrary polygons
- Geometric interpretation: Relates to the cross product of vectors
Angle Calculation through Vector Calculation
Form Vectors
From the coordinates of the vertices, side vectors are formed that represent direction and length of triangle sides.
Dot Product
The dot product of two vectors provides the cosine of the included angle.
Law of Cosines
Alternatively, angles can also be calculated via the law of cosines from the three side lengths.
Completeness
All three interior angles can be calculated independently, check via angle sum = 180°.
Practical Applications
Coordinate-based triangle calculations have diverse applications:
- Computer graphics: 3D modeling, surface triangulation
- Surveying: GPS navigation, land surveying, cartography
- Engineering: Finite element methods, structural analysis
- Astronomy: Position determination of celestial bodies
- Robotics: Path planning, collision detection
- Game development: Collision queries, line of sight calculations
Mathematical Elegance
The analytical treatment of triangles shows the beauty of mathematics:
Unification
Geometric and algebraic methods are combined into a unified approach.
Automation
Complex geometric calculations become systematic algebraic procedures.
Generalization
The methods work in arbitrary dimensions and for complex geometric objects.
Precision
Exact calculations without the inaccuracies of geometric constructions.
Historical Development
Analytical geometry was developed in the 17th century:
- René Descartes (1596-1650): Founder of analytical geometry
- Pierre de Fermat (1601-1665): Developed similar methods in parallel
- Cartesian system: Named after Descartes (Cartesius)
- Revolution: Unification of algebra and geometry
- Foundation: For later development of infinitesimal calculus
Advantages of the Coordinate-Based Method
Computational Advantages
- Systematic, repeatable procedures
- Ideal for computer implementation
- No geometric constructions needed
- Exact results with exact inputs
Educational Advantages
- Connects algebra and geometry
- Shows practical application of mathematics
- Prepares for higher mathematics
- Develops abstract thinking
Summary
The calculation of triangles from coordinates of their vertices is a perfect example of the power of analytical geometry. It connects intuitive geometric concepts with precise algebraic methods and forms the foundation for many modern applications in science and technology.
|
|
Bisector of a triangle • Equilateral triangle • Right triangles • Right triangle, given 1 side and 1 angle • Isosceles right triangles • Isosceles triangles • Triangle area, given 2 sides and 1 anglee • Triangle area, given 1 side and 2 angles • Triangle, Incircle, given 3 sides • Area of a triangle given base and height • Triangle vertices, 3 x/y points •