Dreieck im Koordinatensystem berechnen
Analytische Geometrie: Berechnung von Dreiecken aus Koordinaten der Eckpunkte
Koordinaten-Dreieck Rechner
Analytische Geometrie
Berechnung aller Eigenschaften eines Dreiecks aus den Koordinaten der drei Eckpunkte. Nutzt Vektorrechnung und analytische Methoden.
Koordinatensystem
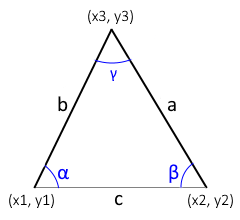
Das Dreieck wird durch drei Punkte A, B, C im kartesischen Koordinatensystem definiert.
Alle geometrischen Eigenschaften werden analytisch berechnet.
Dreieck im Koordinatensystem
Ein Dreieck im Koordinatensystem wird vollständig durch drei Punkte definiert:
- Punkt A (x₁, y₁): Erster Eckpunkt des Dreiecks
- Punkt B (x₂, y₂): Zweiter Eckpunkt des Dreiecks
- Punkt C (x₃, y₃): Dritter Eckpunkt des Dreiecks
- Analytische Berechnung: Alle Eigenschaften aus Koordinaten
- Vektorrechnung: Seitenlängen und Winkel
- Determinanten: Flächenberechnung
Analytische Geometrie Methoden
Die analytische Geometrie ermöglicht präzise Berechnungen mit Koordinaten:
Abstandsformel
- Seitenlängen aus Koordinatendifferenzen
- Anwendung des Satzes von Pythagoras
- d = √[(x₂-x₁)² + (y₂-y₁)²]
- Präzise Berechnung aller drei Seiten
Flächenformel
- Determinanten-basierte Berechnung
- Shoelace-Formel (Gaußsche Trapezformel)
- A = ½|x₁(y₂-y₃) + x₂(y₃-y₁) + x₃(y₁-y₂)|
- Berücksichtigt Orientierung automatisch
Vektorrechnung und Winkel
Vektoren und das Skalarprodukt ermöglichen Winkelberechnungen:
Vektoren bilden
- Seitenvektoren aus Punktdifferenzen
- Vektor AB = (x₂-x₁, y₂-y₁)
- Betrag |AB| = Seitenlänge
- Richtung und Länge kombiniert
Winkel berechnen
- Skalarprodukt zweier Vektoren
- cos(α) = (u⃗ · v⃗) / (|u⃗| |v⃗|)
- Anwendung des Cosinussatzes
- Alle drei Innenwinkel berechenbar
Berechnungsalgorithmus
Der Rechner verwendet einen systematischen Ansatz für die Berechnung:
Schritt 1
Seitenlängen mit Abstandsformel berechnen
Schritt 2
Fläche mit Determinanten-Formel
Schritt 3
Winkel mit Cosinussatz
Schritt 4
Umfang als Summe der Seiten
Formeln für Koordinaten-Dreiecke
Flächeninhalt A
Determinanten-Formel (Shoelace-Formel)
Umfang U
Summe aller drei Seitenlängen
Seitenlängen (Abstandsformel)
\[a = \sqrt{(x_2-x_3)^2 + (y_2-y_3)^2}\]
\[b = \sqrt{(x_1-x_3)^2 + (y_1-y_3)^2}\]
\[c = \sqrt{(x_1-x_2)^2 + (y_1-y_2)^2}\]
Winkel (Cosinussatz)
\[\alpha = \arccos\left(\frac{b^2+c^2-a^2}{2bc}\right)\]
\[\beta = \arccos\left(\frac{a^2+c^2-b^2}{2ac}\right)\]
\[\gamma = \arccos\left(\frac{a^2+b^2-c^2}{2ab}\right)\]
Koordinaten und Bezeichnungen
- A(x₁, y₁): Erster Eckpunkt des Dreiecks
- B(x₂, y₂): Zweiter Eckpunkt des Dreiecks
- C(x₃, y₃): Dritter Eckpunkt des Dreiecks
- a, b, c: Seitenlängen (gegenüber den Punkten)
- α, β, γ: Innenwinkel an den Eckpunkten
- A: Flächeninhalt des Dreiecks
- U: Umfang des Dreiecks
- °: Grad (Winkelmaß)
Rechenbeispiel
Gegeben
1. Seitenlängen berechnen
\[ c = \sqrt{(3-(-2))^2 + (3-(-1))^2 }= \sqrt{25 + 16}= \sqrt{41} ≈ 6.40 \]
Pythagoras in Koordinaten
2. Fläche berechnen
Determinanten-Formel
3. Besonderheiten
- Alle Koordinaten: Ganzzahlig
- Orientierung: Automatisch berücksichtigt
- Präzision: Exakte analytische Methoden
- Vollständig: Alle Parameter berechenbar
Analytische Geometrie und Koordinaten-Dreiecke
Die analytische Geometrie (auch Koordinatengeometrie genannt) ist ein fundamentaler Bereich der Mathematik, der geometrische Probleme durch algebraische Methoden löst. Die Berechnung von Dreiecken aus Koordinaten ihrer Eckpunkte zeigt die Eleganz und Mächtigkeit dieses Ansatzes.
Grundlagen der Koordinatengeometrie
Das kartesische Koordinatensystem ermöglicht es, geometrische Objekte algebraisch zu beschreiben:
- Punktdarstellung: Jeder Punkt wird durch ein Koordinatenpaar (x, y) eindeutig bestimmt
- Abstandsmessung: Die Entfernung zwischen Punkten folgt dem Satz des Pythagoras
- Winkelberechnung: Durch Vektorrechnung und Skalarprodukt möglich
- Flächenberechnung: Elegante Formeln mit Determinanten
- Algebraische Methoden: Geometrische Probleme werden zu Rechenaufgaben
Die Abstandsformel
Die Grundlage aller Längenmessungen im Koordinatensystem ist die Abstandsformel:
Herleitung
Die Formel leitet sich direkt aus dem Satz des Pythagoras ab: Ein rechtwinkliges Dreieck mit Katheten |x₂-x₁| und |y₂-y₁| hat die Hypotenuse d.
Anwendung
Jede Seitenlänge des Dreiecks wird als Abstand zwischen zwei seiner Eckpunkte berechnet.
Vorteile
Funktioniert in allen Quadranten, berücksichtigt negative Koordinaten automatisch, liefert immer positive Abstände.
Präzision
Exakte Berechnung ohne Näherungen, solange die Koordinaten exakt sind.
Flächenberechnung mit Determinanten
Die Determinanten-Formel für die Dreiecksfläche ist ein Meisterwerk der analytischen Geometrie:
- Shoelace-Formel: Auch als Gaußsche Trapezformel bekannt
- Orientierung: Der Betrag sorgt dafür, dass die Fläche immer positiv ist
- Effizienz: Direkte Berechnung ohne Umweg über Seitenlängen und Höhen
- Verallgemeinerung: Funktioniert für beliebige Polygone
- Geometrische Interpretation: Bezieht sich auf das Kreuzprodukt von Vektoren
Winkelberechnung durch Vektorrechnung
Vektoren bilden
Aus den Koordinaten der Eckpunkte werden Seitenvektoren gebildet, die Richtung und Länge der Dreiecksseiten repräsentieren.
Skalarprodukt
Das Skalarprodukt zweier Vektoren liefert den Cosinus des eingeschlossenen Winkels.
Cosinussatz
Alternativ können Winkel auch über den Cosinussatz aus den drei Seitenlängen berechnet werden.
Vollständigkeit
Alle drei Innenwinkel können unabhängig berechnet werden, Kontrolle über Winkelsumme = 180°.
Praktische Anwendungen
Koordinaten-basierte Dreiecksberechnungen haben vielfältige Anwendungen:
- Computer-Grafik: 3D-Modellierung, Triangulation von Oberflächen
- Vermessung: GPS-Navigation, Landvermessung, Kartographie
- Ingenieurswesen: Finite-Elemente-Methoden, Strukturanalyse
- Astronomie: Positionsbestimmung von Himmelskörpern
- Robotik: Pfadplanung, Kollisionserkennung
- Spieleentwicklung: Kollisionsabfragen, Sichtlinienberechnungen
Mathematische Eleganz
Die analytische Behandlung von Dreiecken zeigt die Schönheit der Mathematik:
Vereinheitlichung
Geometrische und algebraische Methoden werden zu einem einheitlichen Ansatz verbunden.
Automatisierung
Komplexe geometrische Berechnungen werden zu systematischen algebraischen Verfahren.
Verallgemeinerung
Die Methoden funktionieren in beliebigen Dimensionen und für komplexe geometrische Objekte.
Präzision
Exakte Berechnungen ohne die Ungenauigkeiten geometrischer Konstruktionen.
Historische Entwicklung
Die analytische Geometrie wurde im 17. Jahrhundert entwickelt:
- René Descartes (1596-1650): Begründer der analytischen Geometrie
- Pierre de Fermat (1601-1665): Parallel entwickelte ähnliche Methoden
- Kartesisches System: Benannt nach Descartes (Cartesius)
- Revolution: Vereinigung von Algebra und Geometrie
- Grundlage: Für die spätere Entwicklung der Infinitesimalrechnung
Vorteile der koordinatenbasierten Methode
Rechnerische Vorteile
- Systematische, wiederholbare Verfahren
- Ideal für Computerimplementierung
- Keine geometrischen Konstruktionen nötig
- Exakte Ergebnisse bei exakten Eingaben
Pädagogische Vorteile
- Verbindet Algebra und Geometrie
- Zeigt praktische Anwendung der Mathematik
- Bereitet auf höhere Mathematik vor
- Entwickelt abstraktes Denken
Zusammenfassung
Die Berechnung von Dreiecken aus Koordinaten ihrer Eckpunkte ist ein perfektes Beispiel für die Macht der analytischen Geometrie. Sie verbindet intuitive geometrische Konzepte mit präzisen algebraischen Methoden und bildet die Grundlage für viele moderne Anwendungen in Wissenschaft und Technik.
|
|