Gleichschenkliges, rechtwinkliges Dreieck
45°-45°-90° Dreieck: Symmetrie und rechter Winkel in perfekter Kombination
Isoszeles Rechner
45°-45°-90° Dreieck
Ein gleichschenkliges rechtwinkliges Dreieck hat einen rechten Winkel (90°) und zwei 45°-Winkel. Die beiden Katheten sind gleich lang.
45°-45°-90° Dreieck
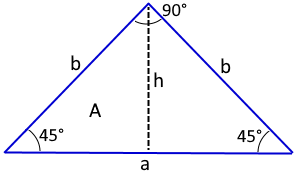
Gleichschenkliges rechtwinkliges Dreieck mit zwei gleichen Katheten.
Die Winkel betragen 45°, 45° und 90°.
Besondere Eigenschaften
Katheten: Beide gleich lang
Symmetrie: Spiegelachse durch Höhe
Was ist ein gleichschenkliges rechtwinkliges Dreieck?
Ein gleichschenkliges rechtwinkliges Dreieck vereint zwei besondere Eigenschaften:
- Rechtwinklig: Ein Winkel beträgt exakt 90°
- Gleichschenklig: Zwei Seiten sind gleich lang (die Katheten)
- 45°-Winkel: Die beiden spitzen Winkel betragen je 45°
- Symmetrie: Spiegelachse durch die Höhe zur Hypotenuse
- Verhältnis: Seitenverhältnis 1:1:√2
- Anwendung: Häufig in Technik und Architektur
Symmetrie und Gleichheit
Die Symmetrie verleiht diesem Dreieck besondere Eigenschaften:
Gleiche Katheten
- Beide Katheten haben identische Länge
- Bilden einen rechten Winkel (90°)
- Stehen senkrecht aufeinander
- Symmetrische Anordnung zum rechten Winkel
Spiegelachse
- Höhe zur Hypotenuse ist Symmetrieachse
- Teilt das Dreieck in zwei kongruente Hälften
- Halbiert die Hypotenuse im rechten Winkel
- Jede Hälfte ist ein rechtwinkliges Dreieck
Die 45°-Winkel
Die beiden 45°-Winkel sind das charakteristische Merkmal:
Winkeleigenschaften
- Beide spitzen Winkel sind identisch (45°)
- Ergänzen sich zum rechten Winkel (45° + 45° = 90°)
- Winkelsumme: 45° + 45° + 90° = 180°
- Komplementäre Winkel zueinander
Trigonometrische Werte
- sin(45°) = cos(45°) = √2/2 ≈ 0.707
- tan(45°) = 1 (perfekte Symmetrie)
- Einheitskreis: 45° = π/4 Radiant
- Exakte Werte ohne Näherungen
Besonderes Dreieck in der Mathematik
Das 45°-45°-90° Dreieck gehört zu den wichtigsten Dreiecken:
Seitenverhältnis
Kathete : Kathete : Hypotenuse
Wurzel von 2
Hypotenuse = Kathete × √2
Einfache Formeln
Höhe = halbe Hypotenuse
Formeln für gleichschenklige rechtwinklige Dreiecke
Grundformeln
Kathete: \( \ \displaystyle a = \frac{b}{\sqrt{2}}\)
Verhältnis 1:√2 zwischen Kathete und Hypotenuse
Höhe zur Hypotenuse
Höhe ist die Hälfte der Basis (Hypotenuse)
Fläche
Viertel des Quadrats der Hypotenuse
Umfang
Hypotenuse mal (1 + √2)
Alternative Formeln
\[a = b\sqrt{2}\], \[h = \frac{b\sqrt{2}}{2}\]
\[a = 2h\], \[b = h\sqrt{2}\]
\[a = 2\sqrt{A}\], \[b = \sqrt{2A}\]
\[b = \frac{a}{\sin(45°)} = \frac{a}{\cos(45°)}\]
Bezeichnungen und Symbole
- a: Hypotenuse (Basis, längste Seite)
- b: Kathete (beide Katheten gleich lang)
- h: Höhe zur Hypotenuse
- A: Flächeninhalt
- U: Umfang
- √2: Wurzel aus 2 ≈ 1.414
- 45°: Die beiden spitzen Winkel
- 90°: Der rechte Winkel
Rechenbeispiel
Gegeben
Gleichschenkliges rechtwinkliges Dreieck
1. Katheten berechnen
Beide Katheten sind gleich lang
2. Höhe berechnen
Höhe ist halbe Hypotenuse
3. Fläche berechnen
Viertel des Hypotenusen-Quadrats
4. Umfang berechnen
Hypotenuse plus beide Katheten
Kontrolle
- Pythagoras: (5√2)² + (5√2)² = 50 + 50 = 100 = 10² ✓
- Winkel: 45° + 45° + 90° = 180° ✓
- Verhältnis: 7.07:7.07:10 ≈ 1:1:√2 ✓
Das gleichschenklige rechtwinklige Dreieck in Mathematik und Praxis
Das gleichschenklige rechtwinklige Dreieck (auch 45°-45°-90° Dreieck genannt) ist eines der wichtigsten speziellen Dreiecke in der Mathematik. Es vereint die Eigenschaften eines rechtwinkligen Dreiecks mit der Symmetrie eines gleichschenkligen Dreiecks und bildet dadurch eine perfekte Brücke zwischen Geometrie, Algebra und praktischen Anwendungen.
Geometrische Eigenschaften und Symmetrie
Die besondere Kombination von rechtem Winkel und Gleichschenkligkeit verleiht diesem Dreieck einzigartige Eigenschaften:
- Doppelte Symmetrie: Sowohl punkt- als auch achsensymmetrisch bezüglich der Höhe zur Hypotenuse
- Perfekte Winkelverteilung: 45°-45°-90° ergibt eine harmonische Aufteilung
- Kongruente Hälften: Die Höhe teilt das Dreieck in zwei identische rechtwinklige Dreiecke
- Isometrische Katheten: Beide Katheten haben exakt dieselbe Länge
- Optimale Proportionen: Das Seitenverhältnis 1:1:√2 ist mathematisch elegant
Das Verhältnis 1:1:√2 und seine Bedeutung
Das charakteristische Seitenverhältnis hat tiefe mathematische Bedeutung:
Mathematische Eleganz
Die Wurzel aus 2 (√2 ≈ 1.414) tritt natürlich auf, wenn aus einem Quadrat durch Diagonalteilung zwei Dreiecke entstehen.
Pythagorisches Theorem
Perfekte Demonstration: a² + a² = (a√2)², zeigt die Anwendung des Satzes von Pythagoras in Reinform.
Geometrische Konstruktion
Einfach konstruierbar: Quadrat diagonal teilen oder gleichseitiges Dreieck modifizieren.
Irrationale Zahl
√2 ist die erste historisch bekannte irrationale Zahl, entdeckt von den Pythagoräern.
Trigonometrische Besonderheiten
Die 45°-Winkel ergeben besondere trigonometrische Werte:
Exakte Werte
- sin(45°) = cos(45°) = √2/2 ≈ 0.7071
- tan(45°) = 1 (perfekte Symmetrie)
- Keine Näherungen nötig: algebraisch exakt
- Einheitskreis: 45° = π/4 Radiant
Funktionale Beziehungen
- sin(45°) = cos(45°): perfekte Symmetrie
- tan(45°) = 1: Steigung von 45° ist 1:1
- Komplementäre Gleichheit bei 45°
- Grundlage für trigonometrische Identitäten
Praktische Anwendungen
Das 45°-45°-90° Dreieck ist in der Praxis allgegenwärtig:
Architektur und Bauwesen
- Dachneigungen: 45° für optimale Entwässerung
- Treppen: Standardsteigung für Komfort
- Eckverbindungen: Gehrungsschnitte bei 45°
- Fundamentgräben: Böschungswinkel
Design und Kunst
- Diagonale Kompositionen
- Goldener Schnitt Ableitungen
- Symmetrische Gestaltungen
- Optische Ausgewogenheit
Technik und Ingenieurswesen
- Maschinenbau: Fasen und Kanten
- Optik: Strahlenteilung bei 45°
- Elektronik: Kristallstrukturen
- Navigation: Kursberechnungen
Informatik und Grafik
- Pixelraster: diagonale Linien
- 3D-Grafik: Standardrotationen
- Bildverarbeitung: Kantenfilter
- Spieleentwicklung: Bewegungsrichtungen
Historische und kulturelle Bedeutung
Antike Mathematik
Schon die Babylonier und Ägypter nutzten 45°-Dreiecke für Konstruktionen und stellten fest, dass die Diagonale eines Quadrats inkommensurabel zu seiner Seite ist.
Pythagoräische Schule
Die Entdeckung der Irrationalität von √2 am gleichschenkligen rechtwinkligen Dreieck führte zur ersten Krise in der griechischen Mathematik.
Buddhistische Kultur
In der buddhistischen Architektur symbolisiert der 45°-Winkel die Balance zwischen Himmel und Erde.
Moderne Mathematik
Grundlage für komplexe Zahlen, Rotationen in der Ebene und Fourieranalyse.
Konstruktion und Zeichnung
Das gleichschenklige rechtwinklige Dreieck lässt sich auf verschiedene Weise konstruieren:
- Aus dem Quadrat: Diagonale teilt Quadrat in zwei kongruente Dreiecke
- Mit Zirkel und Lineal: Rechter Winkel + gleiche Katheten
- Über 45°-Winkel: Winkelhalbierung des rechten Winkels
- Koordinatengeometrie: Punkte (0,0), (a,0), (0,a) verbinden
- Falttechnik (Origami): Quadrat diagonal falten
Verallgemeinerungen und Erweiterungen
Höhere Dimensionen
In 3D entspricht es der halben Diagonalen eines Würfels, in n-dimensionalen Räumen entstehen ähnliche Verhältnisse.
Fraktale Geometrie
Sierpinski-Dreieck und andere Fraktale nutzen die Selbstähnlichkeit des 45°-45°-90° Dreiecks.
Komplexe Zahlen
Die 45°-Rotation entspricht der Multiplikation mit (1+i)/√2 in der komplexen Ebene.
Kristallographie
Kubische Kristallsysteme zeigen häufig 45°-Winkel in ihren Spaltebenen.
Didaktische Bedeutung
In der Mathematikdidaktik ist das gleichschenklige rechtwinklige Dreieck von besonderer Bedeutung:
- Einführung irrationaler Zahlen: √2 als erstes Beispiel
- Pythagoras-Verständnis: Anschauliche Demonstration des Theorems
- Trigonometrie-Grundlagen: Exakte Werte ohne Taschenrechner
- Symmetrie-Konzepte: Mehrfache Symmetrieeigenschaften
- Konstruktions-Übungen: Einfache und elegante Konstruktionen
Zusammenfassung
Das gleichschenklige rechtwinklige Dreieck ist ein Meisterwerk der geometrischen Eleganz. Es verbindet fundamentale mathematische Konzepte wie irrationale Zahlen, trigonometrische Funktionen und Symmetrie in einer einzigen, einfachen Form. Seine praktische Relevanz reicht von der antiken Architektur bis zur modernen Computergrafik und macht es zu einem der wichtigsten speziellen Dreiecke der Mathematik.
|
|