Gleichseitiges Dreieck berechnen
Online Rechner und Formeln für das perfekt symmetrische Dreieck
Gleichseitiges Dreieck Rechner
Perfekte Symmetrie
Ein gleichseitiges Dreieck hat drei gleiche Seiten und Winkel (je 60°). Es ist das einfachste regelmäßige Polygon.
Visualisierung
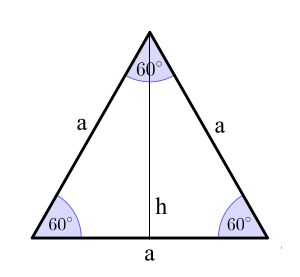
Das gleichseitige Dreieck mit drei gleichen Seiten a und drei 60°-Winkeln.
Alle Höhen, Mittelsenkrechten und Winkelhalbierenden treffen sich im Zentrum.
Was ist ein gleichseitiges Dreieck?
Ein gleichseitiges Dreieck ist die perfekteste Form eines Dreiecks:
- Drei gleiche Seiten: Alle Seiten haben die Länge a
- Drei gleiche Winkel: Jeder Winkel beträgt exakt 60°
- Regelmäßiges Polygon: Das einfachste regelmäßige Vieleck
- Perfekte Symmetrie: Drei Symmetrieachsen
- Anwendung: Natur, Architektur, Kristalle, Design
- Berechnung: Aus einem Parameter alle anderen ableitbar
Perfekte dreifache Symmetrie
Die dreifache Symmetrie macht das gleichseitige Dreieck einzigartig:
Drei Symmetrieachsen
- Jede Höhe ist eine Symmetrieachse
- Gleichzeitig Mittelsenkrechte und Winkelhalbierende
- Teilt das Dreieck in zwei kongruente Hälften
- 120° Drehsymmetrie um das Zentrum
Zentrale Punkte
- Schwerpunkt, Umkreis- und Inkreismittelpunkt fallen zusammen
- Alle Höhen treffen sich im Zentrum
- Zentrum teilt jede Höhe im Verhältnis 2:1
- Perfekte Balance in allen Richtungen
Regelmäßiges Polygon
Als regelmäßiges Polygon hat das gleichseitige Dreieck besondere Eigenschaften:
Gleichmäßigkeit
- Alle Seiten gleich lang
- Alle Winkel gleich groß
- Perfekte Regelmäßigkeit
Drehsymmetrie
- 120° Drehsymmetrie
- 3-fache Rotationssymmetrie
- Invariant unter Drehung
Kreise
- Umkreis und Inkreis konzentrisch
- Einfache Radius-Beziehungen
- Optimale Flächennutzung
Konstruktion mit Zirkel und Lineal
Das gleichseitige Dreieck lässt sich elegant mit Zirkel und Lineal konstruieren:
Konstruktionsschritte
- Basis zeichnen: Zeichnen Sie eine Strecke AB der gewünschten Länge
- Kreise schlagen: Um A und B jeweils einen Kreis mit Radius AB
- Schnittpunkt finden: Die Kreise schneiden sich in zwei Punkten
- Dreieck vollenden: Verbinden Sie einen Schnittpunkt mit A und B

Konstruktion mit Zirkel
Formeln zum gleichseitigen Dreieck
Fläche A
Klassische Formel mit √3
Umfang P
Einfachste Formel - drei gleiche Seiten
Höhe h
Höhe aus Seitenlänge
Seitenlänge a
Seite aus Höhe
Alternative Formeln
Kreise und besondere Punkte
- Umkreisradius: \(R = \frac{a}{\sqrt{3}}\)
- Inkreisradius: \(r = \frac{a\sqrt{3}}{6}\)
- Höhen-Schnittpunkt: \(\frac{2h}{3}\) von jeder Ecke
- Alle Winkel: 60° (π/3 rad)
- Verhältnis R:r: 2:1
- Schwerpunkt = Zentrum: Alle besonderen Punkte fallen zusammen
Die magische Zahl √3
Die Quadratwurzel aus 3 (≈ 1.732) erscheint in fast allen Formeln des gleichseitigen Dreiecks. Sie resultiert aus den 60°-Winkeln und den trigonometrischen Beziehungen: sin(60°) = √3/2, cos(60°) = 1/2, tan(60°) = √3.
Rechenbeispiel
Gegeben
1. Höhe berechnen
Die charakteristische √3-Beziehung
2. Fläche berechnen
Optimal effiziente Flächennutzung
3. Umfang berechnen
Einfachste Berechnung
4. Besondere Eigenschaften
- Alle Winkel: 60°
- Umkreisradius: R ≈ 5.77
- Inkreisradius: r ≈ 2.89
- Perfekte Symmetrie
Das gleichseitige Dreieck in Natur und Kultur
Das gleichseitige Dreieck ist nicht nur das perfekteste aller Dreiecke, sondern auch eine der fundamentalsten Formen in Natur, Wissenschaft und Kultur. Seine dreifache Symmetrie und die eleganten mathematischen Beziehungen machen es zu einem Symbol für Vollkommenheit und Harmonie.
Mathematische Perfektion
Als regelmäßiges Polygon mit der geringsten Seitenzahl verkörpert das gleichseitige Dreieck mathematische Eleganz:
- Minimale Komplexität: Das einfachste regelmäßige Polygon (n=3)
- Maximale Symmetrie: Drei Symmetrieachsen und 120°-Drehsymmetrie
- Optimale Verhältnisse: Beste Flächen-zu-Umfang-Relation unter allen Dreiecken
- Einheitliche Winkel: Alle Innenwinkel = 60° = π/3 rad
- Zentrale Konvergenz: Alle besonderen Punkte fallen im Zentrum zusammen
Erscheinungsformen in der Natur
Die Natur nutzt das gleichseitige Dreieck als Grundbaustein für stabile und effiziente Strukturen:
Kristallstrukturen
Viele Mineralien kristallisieren in dreieckigen Gittern, die auf gleichseitigen Dreiecken basieren.
Biologische Strukturen
Bienenwaben, Diatomeen, Radiolarienskelette nutzen dreieckige Grundstrukturen für maximale Stabilität.
Molekulare Geometrie
Viele Moleküle haben trigonal-planare Struktur (z.B. Borverbindungen, bestimmte Kohlenstoffverbindungen).
Physikalische Phänomene
Interferenzmuster, Kraftverteilungen und Strömungen zeigen oft dreieckige Symmetrien.
Kulturelle und historische Bedeutung
Das gleichseitige Dreieck hat tiefe symbolische Bedeutung in verschiedenen Kulturen:
- Mystik und Religion: Symbol der Trinität, Vollkommenheit und göttlichen Ordnung
- Alchemie: Repräsentiert die Elemente Feuer (Spitze nach oben) und Wasser (Spitze nach unten)
- Architektur: Grundlage für stabile Konstruktionen, von Pyramiden bis zu modernen Stahlbauten
- Kunst und Design: Grundform für harmonische Kompositionen und ästhetische Proportionen
- Flaggen und Heraldik: Symbol für Stärke, Stabilität und Einheit
Technische und praktische Anwendungen
Konstruktion und Architektur
Dreieckige Fachwerke, Brückenkonstruktionen und Dachsysteme nutzen die inhärente Stabilität des Dreiecks.
Ingenieurswesen
Triangulation in der Vermessung, Finite-Elemente-Methoden, Strukturanalyse verwenden dreieckige Grundelemente.
Computer-Grafik
3D-Modelle werden als Dreiecksnetze (Meshes) dargestellt, da Dreiecke immer planar sind.
Optik und Elektronik
Prisma-Optik, Kristalloszillatoren und Mikrowellen-Antennen nutzen dreieckige Geometrien.
Mathematische Verwandtschaften
Das gleichseitige Dreieck steht im Zentrum vieler mathematischer Konzepte:
- Trigonometrie: Die 30°-60°-90° Beziehungen leiten sich vom halbierten gleichseitigen Dreieck ab
- Platonische Körper: Grundlage für Tetraeder und Oktaeder
- Tessellierungen: Ermöglicht perfekte Parkettierungen der Ebene
- Fraktale Geometrie: Sierpinski-Dreieck als selbstähnliche Struktur
- Komplexe Zahlen: Die dritten Einheitswurzeln bilden ein gleichseitiges Dreieck
Optimierungseigenschaften
Das gleichseitige Dreieck ist in vieler Hinsicht optimal:
Isoperimetrisches Problem
Unter allen Dreiecken mit gleichem Umfang hat das gleichseitige die größte Fläche.
Strukturelle Effizienz
Bietet maximale Stabilität bei minimalem Materialaufwand in Fachwerkkonstruktionen.
Packungsdichte
Ermöglicht die dichteste Packung von Kreisen in der Ebene (hexagonale Packung).
Symmetrie-Effizienz
Maximale Rotationssymmetrie (120°) bei minimaler Seitenzahl (3).
Pädagogische Bedeutung
In der Mathematikausbildung spielt das gleichseitige Dreieck eine zentrale Rolle:
- Geometrie-Grundlagen: Einführung in Symmetrie, regelmäßige Formen und Konstruktion
- Trigonometrie: Herleitung der Grundwerte für 30°, 60° und √3-Beziehungen
- Analytische Geometrie: Koordinatengeometrie und Vektorrechnung
- Zahlentheorie: Einheitswurzeln und komplexe Zahlen
- Anwendungsmathematik: Optimierung, Modellierung und numerische Methoden
Zusammenfassung
Das gleichseitige Dreieck ist weit mehr als nur eine geometrische Form. Es ist ein fundamentales mathematisches Objekt, das Einfachheit mit Perfektion verbindet, praktische Anwendungen ermöglicht und tiefe theoretische Einsichten bietet. Seine universelle Präsenz in Natur, Technik und Kultur macht es zu einem der wichtigsten geometrischen Grundbausteine unserer Welt.
|
|