Flächeninhalt eines Dreiecks berechnen
Berechnung der Fläche eines Dreiecks aus drei Seiten nach Herons Formel
Heron-Formel Rechner
Heronsche Flächenformel
Die Heron-Formel berechnet die Fläche aus drei Seitenlängen ohne Winkel oder Höhen zu benötigen.
Visualisierung
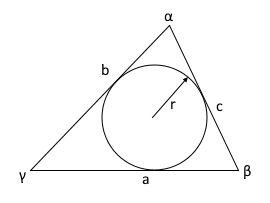
Das Diagramm zeigt ein Dreieck mit allen drei Seiten a, b, c und dem Inkreis.
Die Heron-Formel berechnet die Fläche nur aus den Seitenlängen.
Dreiecksungleichung beachten
Jede Seite muss kleiner als die Summe der beiden anderen sein: a < b + c, b < a + c, c < a + b
Was ist die Heron-Formel?
Die Heron-Formel ist eine der elegantesten Methoden der Geometrie:
- Nur Seitenlängen: Keine Winkel oder Höhen erforderlich
- Universell: Funktioniert für alle Dreieckstypen
- Komplett: Bestimmt alle weiteren Eigenschaften des Dreiecks
- Historisch: Benannt nach Heron von Alexandria (1. Jh. n. Chr.)
- Anwendung: Vermessung, CAD, Materialberechnung
- Basis: Für weitere Berechnungen wie Inkreis und Winkel
Der Inkreis des Dreiecks
Der Inkreis ist der größte Kreis, der vollständig im Dreieck liegt:
Eigenschaften des Inkreises
- Berührt alle drei Seiten des Dreiecks
- Mittelpunkt liegt im Schnittpunkt der Winkelhalbierenden
- Radius r = Fläche / Halbumfang
- Optimale Nutzung des Dreiecks-Innenraums
Berechnung über Heron
- Fläche A über Heron-Formel
- Halbumfang s = (a + b + c) / 2
- Inkreis-Radius r = A / s
- Inkreis-Fläche = π × r²
Berechnungsschritte verstehen
Die Heron-Berechnung erfolgt in systematischen Schritten:
1. Validierung
Prüfung der Dreiecksungleichung für alle drei Seiten
2. Halbumfang
s = (a + b + c) / 2 als Grundlage für alle weiteren Berechnungen
3. Heron-Formel
A = √[s(s-a)(s-b)(s-c)] für die Flächenberechnung
4. Weitere Werte
Winkel über Kosinussatz, Höhen und Inkreis-Eigenschaften
Heron-Formel und weitere Berechnungen
Die klassische Heron-Formel
Alternative Heron-Formeln
Inkreis-Berechnungen
Winkel α
Winkel β
Winkel γ
Höhe berechnen
Höhe zur Seite a
Umkreis-Radius
Radius des Umkreises
Symbole und Bezeichnungen
- A: Flächeninhalt des Dreiecks
- a, b, c: Seitenlängen des Dreiecks
- s: Halbumfang (a+b+c)/2
- α, β, γ: Innenwinkel des Dreiecks
- r: Inkreis-Radius
- R: Umkreis-Radius
- h: Höhe des Dreiecks
- √: Quadratwurzel (charakteristisch für Heron)
Rechenbeispiel
Gegeben
1. Halbumfang
Halbumfang s = 6
2. Heron-Formel
Die Fläche beträgt 6 Flächeneinheiten
3. Inkreis
Inkreis-Radius r = 1, Fläche = π ≈ 3,14
4. Besonderheit
Dies ist ein rechtwinkliges Dreieck!
3² + 4² = 9 + 16 = 25 = 5²
Kontrolle: A = ½ × 3 × 4 = 6 ✓
5. Winkel
β ≈ 53,13°
γ ≈ 36,87°
Die Heron-Formel in Mathematik und Anwendung
Die Heron-Formel (auch Heronsche Flächenformel) ist eine der bemerkenswertesten Entdeckungen der antiken Mathematik. Sie ermöglicht die Berechnung der Dreiecksfläche ausschließlich aus den drei Seitenlängen, ohne dass Winkel, Höhen oder andere geometrische Konstruktionen erforderlich sind.
Historischer Hintergrund
Die Formel trägt den Namen des alexandrinischen Mathematikers Heron (ca. 10-70 n. Chr.):
- Heron von Alexandria: Griechischer Mathematiker und Ingenieur der Antike
- Überlieferung: Erste systematische Darstellung in "Metrica" (ca. 60 n. Chr.)
- Frühere Ursprünge: Möglicherweise bereits Archimedes bekannt (287-212 v. Chr.)
- Chinesische Mathematik: Ähnliche Formeln in "Liu Hui" (3. Jh. n. Chr.)
- Moderne Bedeutung: Fundamentaler Baustein der analytischen Geometrie
Mathematische Struktur und Eleganz
Symmetrische Form
Die Formel A = √[s(s-a)(s-b)(s-c)] zeigt perfekte Symmetrie bezüglich aller drei Seitenlängen. Jede Seite wird gleichberechtigt behandelt.
Quadratwurzel-Charakter
Die charakteristische Wurzel macht die Formel einzigartig unter den Flächenformeln und verleiht ihr ihre besondere mathematische Eleganz.
Halbumfang als Schlüssel
Der Halbumfang s = (a+b+c)/2 ist der zentrale Parameter, der alle geometrischen Eigenschaften des Dreiecks kodiert.
Produktform
Das Produkt s(s-a)(s-b)(s-c) enthält alle Informationen über die Form und Größe des Dreiecks in kompakter Form.
Geometrische Interpretation
Die Terme (s-a), (s-b), (s-c) haben eine anschauliche geometrische Bedeutung:
- s-a: "Überschuss" des Halbumfangs über die Seite a
- s-b: "Überschuss" des Halbumfangs über die Seite b
- s-c: "Überschuss" des Halbumfangs über die Seite c
- Produkt: Kodiert die "Ausgeglichenheit" der Seitenverhältnisse
Praktische Anwendungen
Die Heron-Formel findet breite Anwendung in verschiedenen Bereichen:
- Landvermessung: Flächenberechnung unregelmäßiger Grundstücke
- Bauplanung: Materialberechnung für dreieckige Konstruktionen
- CAD-Software: Automatische Flächenberechnung in technischen Zeichnungen
- Geodäsie: Triangulation und Geländeaufnahme
- Computergrafik: Polygon-Flächenberechnung und Mesh-Analyse
- Physik: Querschnittsberechnungen und Materialwissenschaft
Verwandte Berechnungen
Die Heron-Formel ist der Ausgangspunkt für viele weitere Dreiecksberechnungen:
Inkreis-Eigenschaften
- Inkreis-Radius: r = A/s
- Inkreis-Fläche: π × r²
- Berührungspunkte auf den Seiten
- Optimale Kreiseinbeschreibung
Weitere Eigenschaften
- Höhen: h = 2A/Seite
- Winkel über Kosinussatz
- Umkreis-Radius: R = abc/(4A)
- Schwerpunkt und andere Zentren
Alternative Formulierungen
Die Heron-Formel kann in verschiedenen mathematisch äquivalenten Formen dargestellt werden:
- Klassische Form: A = √[s(s-a)(s-b)(s-c)]
- Erweiterte Form: A = ¼√[(a+b+c)(-a+b+c)(a-b+c)(a+b-c)]
- Determinanten-Form: A = ¼√[4a²b² - (a²+b²-c²)²]
- Brahmagupta-Verallgemeinerung: Für Vierecke (bei zyklischen Vierecken)
Numerische Aspekte
Bei der praktischen Anwendung sind verschiedene numerische Überlegungen wichtig:
- Dreiecksungleichung: Obligatorische Prüfung vor der Berechnung
- Numerische Stabilität: Probleme bei sehr "dünnen" Dreiecken
- Rundungsfehler: Verstärkung bei ungünstigen Seitenverhältnissen
- Alternative Algorithmen: Kahan-Formel für bessere numerische Eigenschaften
Verallgemeinerungen und Erweiterungen
Höhere Dimensionen
Verallgemeinerungen für Tetraeder (Cayley-Menger-Determinante) und höherdimensionale Simplexe in der analytischen Geometrie.
Sphärische Geometrie
Anpassungen für Dreiecke auf Kugeloberflächen mit entsprechend modifizierten trigonometrischen Beziehungen.
Hyperbolische Geometrie
Varianten für nicht-euklidische Geometrien mit angepassten Abstandsbegriffen und Winkeldefinitionen.
Computeralgebra
Symbolische Berechnungen und exakte Arithmetik für theoretische Untersuchungen und Beweise.
Moderne Bedeutung
In der heutigen Mathematik und Technik bleibt die Heron-Formel hochrelevant:
- Algorithmische Geometrie: Grundbaustein für Computational Geometry
- Finite Elemente: Flächenberechnung in numerischen Simulationen
- Computer Vision: Objekterkennung und 3D-Rekonstruktion
- Robotik: Pfadplanung und Kollisionserkennung
- Spieleentwicklung: Physics Engines und Kollisionsdetection
Zusammenfassung
Die Heron-Formel ist ein Meisterwerk der antiken Mathematik, das bis heute nichts von seiner Eleganz und praktischen Bedeutung verloren hat. Sie verbindet mathematische Schönheit mit praktischer Anwendbarkeit und bildet eine Brücke zwischen klassischer Geometrie und modernen computergestützten Berechnungen. Ihre Einfachheit in der Anwendung bei gleichzeitiger mathematischer Tiefe macht sie zu einem unverzichtbaren Werkzeug für Mathematiker, Ingenieure und Wissenschaftler aller Disziplinen.
|
|