Flächeninhalt eines Dreiecks berechnen
Rechner zur Berechnung der Fläche eines Dreiecks bei gegebener Basis und Höhe
Dreiecksfläche Rechner (Basis × Höhe)
Klassische Flächenformel
Die Dreiecksfläche wird aus Basis und der darauf senkrecht stehenden Höhe berechnet.
Visualisierung
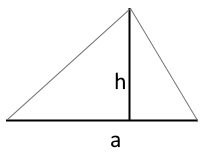
Das Diagramm zeigt ein Dreieck mit Basis a und senkrechter Höhe h.
Die Höhe steht im 90°-Winkel zur Basis.
Was ist die klassische Dreiecksflächen-Formel?
Die klassische Flächenformel ist die grundlegendste Methode zur Dreiecksflächenberechnung:
- Basis: Eine beliebige Seite des Dreiecks
- Höhe: Senkrechte Strecke von der Basis zum gegenüberliegenden Eckpunkt
- 90°-Winkel: Höhe steht immer senkrecht zur Basis
- Formel: A = ½ × Basis × Höhe
- Anwendung: Einfachste und direkteste Berechnung
- Vorteil: Funktioniert für alle Dreieckstypen
Die Höhe im Dreieck verstehen
Die Höhe ist ein fundamentales Element der Dreiecksgeometrie:
Definition der Höhe
- Senkrechte Linie von einem Eckpunkt zur gegenüberliegenden Seite
- Bildet immer einen 90°-Winkel mit der Basis
- Kürzeste Entfernung zwischen Punkt und Gerade
- Kann innerhalb oder außerhalb des Dreiecks liegen
Höhen-Eigenschaften
- Jedes Dreieck hat drei verschiedene Höhen
- Alle drei Höhen schneiden sich im Höhenschnittpunkt
- Bei spitzwinkligen Dreiecken liegen alle Höhen innen
- Bei stumpfwinkligen Dreiecken liegen zwei Höhen außen
Geometrische Interpretation
Die Flächenformel A = ½ × a × h hat eine anschauliche geometrische Bedeutung:
Parallelogramm-Bezug
Ein Dreieck ist genau die Hälfte eines Parallelogramms mit gleicher Basis und Höhe
Teilung eines Rechtecks
Diagonal geteiltes Rechteck ergibt zwei gleiche rechtwinklige Dreiecke
Universelle Gültigkeit
Die Formel gilt für spitzwinklige, rechtwinklige und stumpfwinklige Dreiecke
Formeln für alle drei Höhen
Die drei möglichen Basis-Höhe-Kombinationen
Basis a mit Höhe ha
Basis b mit Höhe hb
Basis c mit Höhe hc
Jede Seite kann als Basis verwendet werden - wichtig ist die entsprechende Höhe
Höhe berechnen
Höhe aus bekannter Fläche und Basis
Basis berechnen
Basis aus bekannter Fläche und Höhe
Höhe über Trigonometrie
\[h = b \cdot \sin(\alpha)\]
Höhe aus anliegender Seite und Winkel
Höhe über Pythagoras
Höhe aus drei Seitenlängen
Symbole und Bezeichnungen
- A: Flächeninhalt des Dreiecks
- a, b, c: Seitenlängen des Dreiecks
- ha, hb, hc: Höhen zu den entsprechenden Seiten
- α, β, γ: Innenwinkel des Dreiecks
- ⊥: Symbol für "senkrecht zu"
- 90°: Rechter Winkel (zwischen Höhe und Basis)
- sin: Sinus-Funktion
- √: Quadratwurzel
Rechenbeispiel
Gegeben
Flächenberechnung
Die Fläche beträgt 35 Flächeneinheiten
Kontrolle
- Plausibilität: Fläche ist positiv
- Vergleich: Kleiner als Rechteck (10×7 = 70)
- Einheit: Quadrateinheiten (z.B. cm²)
Alternative Berechnungen
Alle drei Berechnungen ergeben A = 35
Anwendungen
Grundstücksvermessung, Dachflächen, Materialberechnung, technische Zeichnungen.
Verschiedene Höhen im Dreieck
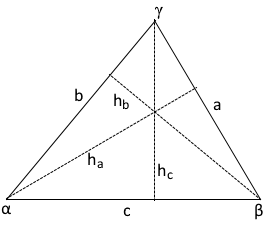
Wichtiger Hinweis: Jede der drei Seiten kann als Basis verwendet werden. Es muss immer die entsprechende Höhe verwendet werden, die senkrecht zu dieser Basis steht. Die Grafik zeigt alle drei möglichen Basis-Höhe-Kombinationen.
Die klassische Dreiecksflächenformel in Theorie und Praxis
Die klassische Flächenformel A = ½ × Basis × Höhe ist die fundamentalste und anschaulichste Methode zur Berechnung von Dreiecksflächen. Sie basiert auf dem grundlegenden geometrischen Prinzip, dass ein Dreieck genau die Hälfte eines Parallelogramms mit gleicher Basis und Höhe ist.
Historische Entwicklung und Bedeutung
Die Formel A = ½ × a × h gehört zu den ältesten mathematischen Erkenntnissen der Menschheit:
- Antike Zivilisationen: Bereits Babylonier und Ägypter verwendeten diese Formel vor über 4000 Jahren
- Praktische Anwendung: Zur Landvermessung und Bauplanung in frühen Hochkulturen
- Euklids Elemente: Systematische Behandlung und Beweis in der griechischen Mathematik
- Moderne Relevanz: Immer noch die wichtigste Grundlage für Flächenberechnungen
Geometrische Interpretation und Verständnis
Parallelogramm-Beziehung
Ein Dreieck ist exakt die Hälfte eines Parallelogramms mit derselben Basis und Höhe. Diese fundamentale Beziehung erklärt den Faktor ½ in der Formel.
Rechteck-Analogie
Bei rechtwinkligen Dreiecken wird diese Beziehung besonders deutlich: Das Dreieck ist die Hälfte eines Rechtecks.
Universelle Gültigkeit
Die Formel funktioniert für alle Dreieckstypen: spitzwinklig, rechtwinklig, stumpfwinklig, gleichschenklig oder unregelmäßig.
Höhen-Konzept
Die Höhe ist immer die kürzeste Verbindung zwischen einem Punkt und der gegenüberliegenden Seite - daher immer senkrecht.
Das Höhen-Konzept verstehen
Die Höhe ist eines der wichtigsten Elemente der Dreiecksgeometrie:
- Definition: Senkrechte Strecke von einem Eckpunkt zur gegenüberliegenden Seite (oder deren Verlängerung)
- Drei Höhen: Jedes Dreieck hat genau drei Höhen - zu jeder Seite eine
- Höhenschnittpunkt: Alle drei Höhen schneiden sich in einem Punkt (Orthozentrum)
- Lage-Abhängigkeit: Bei spitzwinkligen Dreiecken liegen alle Höhen innen, bei stumpfwinkligen zwei außen
Praktische Anwendungen
Die klassische Flächenformel findet breite Anwendung in vielen Bereichen:
- Vermessungswesen: Grundstücksflächen, Triangulation, Geländeaufnahme
- Bauwesen: Dachflächen, Giebel, Konstruktionselemente
- Landwirtschaft: Ackerflächen, Bewässerungsplanung, Ertragsberechnung
- Architektur: Flächenaufteilung, Raumplanung, Materialberechnung
- Computergrafik: Polygon-Rendering, 3D-Modellierung, Flächenanalyse
- Physik: Kräftediagramme, Schwerpunktberechnungen, Momentenberechnung
Berechnungsmethoden der Höhe
Die Höhe kann auf verschiedene Weise bestimmt werden:
Direkte Messung
- Physische Messung mit Maßband oder Messinstrumenten
- Lotrechte Projektion auf die Basis
- Verwendung von rechtwinkligen Hilfsmitteln
Mathematische Berechnung
- Trigonometrie: h = b × sin(α)
- Pythagoras: über rechtwinklige Teildreiecke
- Koordinatengeometrie: Abstandsformel Punkt-Gerade
Vorteile der klassischen Formel
- Anschaulichkeit: Geometrisch sehr gut nachvollziehbar und visualisierbar
- Einfachheit: Nur zwei Parameter erforderlich (Basis und Höhe)
- Präzision: Sehr genaue Ergebnisse bei exakter Höhenmessung
- Universalität: Funktioniert für alle Dreiecksformen
- Grundlage: Basis für viele weiterführende geometrische Berechnungen
Vergleich mit anderen Flächenformeln
Klassische Formel
A = ½ah
Vorteil: Einfach und anschaulich
Nachteil: Höhenmessung erforderlich
Heron-Formel
A = √[s(s-a)(s-b)(s-c)]
Vorteil: Nur Seitenlängen
Nachteil: Komplexere Berechnung
Sinus-Formel
A = ½ab sin(γ)
Vorteil: Zwei Seiten + Winkel
Nachteil: Trigonometrie erforderlich
Fehlerquellen und Genauigkeit
Bei der Anwendung der klassischen Formel sind verschiedene Aspekte zu beachten:
- Höhenmessung: Die Höhe muss exakt senkrecht zur Basis gemessen werden
- Basis-Wahl: Jede Seite kann als Basis dienen - wichtig ist die korrekte Höhe
- Externe Höhen: Bei stumpfwinkligen Dreiecken liegen manche Höhen außerhalb
- Maßeinheiten: Konsistente Einheiten für Basis und Höhe verwenden
- Rundungsfehler: Ausreichende Dezimalstellen für genaue Ergebnisse
Erweiterungen und Verallgemeinerungen
Das Prinzip der klassischen Flächenformel lässt sich erweitern:
- Trapeze: A = ½(a + c) × h (Mittelwert der parallelen Seiten × Höhe)
- Polygone: Zerlegung in Dreiecke und Anwendung der Formel
- 3D-Geometrie: Grundlage für Volumenberechnungen von Pyramiden
- Integration: Verallgemeinerung für krummlinig begrenzte Flächen
Zusammenfassung
Die klassische Dreiecksflächenformel A = ½ × Basis × Höhe ist ein fundamentales Werkzeug der Geometrie, das Einfachheit mit universeller Anwendbarkeit verbindet. Ihre geometrische Anschaulichkeit und praktische Relevanz machen sie zu einem unverzichtbaren Bestandteil der mathematischen Grundausbildung und zu einem wichtigen Hilfsmittel in vielen technischen und wissenschaftlichen Bereichen. Das Verständnis der Höhen-Geometrie und der verschiedenen Berechnungsmöglichkeiten eröffnet den Weg zu weiterführenden geometrischen Konzepten.
|
|