Calculate Triangle Area
Calculator for computing triangle area given base and height
Triangle Area Calculator (Base × Height)
Classic Area Formula
The triangle area is calculated from base and the perpendicular height.
Visualization
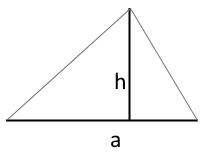
The diagram shows a triangle with base a and perpendicular height h.
The height is at a 90° angle to the base.
What is the Classic Triangle Area Formula?
The classic area formula is the most fundamental method for triangle area calculation:
- Base: Any side of the triangle
- Height: Perpendicular distance from the base to the opposite vertex
- 90° angle: Height is always perpendicular to the base
- Formula: A = ½ × Base × Height
- Application: Simplest and most direct calculation
- Advantage: Works for all triangle types
Understanding Height in Triangles
The height is a fundamental element of triangle geometry:
Definition of Height
- Perpendicular line from a vertex to the opposite side
- Always forms a 90° angle with the base
- Shortest distance between point and line
- Can lie inside or outside the triangle
Height Properties
- Every triangle has three different heights
- All three heights intersect at the orthocenter
- In acute triangles, all heights lie inside
- In obtuse triangles, two heights lie outside
Geometric Interpretation
The area formula A = ½ × a × h has an intuitive geometric meaning:
Parallelogram Relation
A triangle is exactly half of a parallelogram with the same base and height
Rectangle Division
Diagonally divided rectangle yields two equal right triangles
Universal Validity
The formula applies to acute, right, and obtuse triangles
Formulas for All Three Heights
The Three Possible Base-Height Combinations
Base a with height ha
Base b with height hb
Base c with height hc
Any side can be used as base - important is the corresponding height
Calculate Height
Height from known area and base
Calculate Base
Base from known area and height
Height via Trigonometry
Height from adjacent side and angle
Height via Pythagoras
Height from three side lengths
Symbols and Notation
- A: Area of the triangle
- a, b, c: Side lengths of the triangle
- ha, hb, hc: Heights to the corresponding sides
- α, β, γ: Interior angles of the triangle
- ⊥: Symbol for "perpendicular to"
- 90°: Right angle (between height and base)
- sin: Sine function
- √: Square root
Calculation Example
Given
Area Calculation
The area is 35 square units
Verification
- Plausibility: Area is positive
- Comparison: Smaller than rectangle (10×7 = 70)
- Unit: Square units (e.g., cm²)
Alternative Calculations
All three calculations yield A = 35
Applications
Property surveying, roof areas, material calculation, technical drawings.
Different Heights in a Triangle
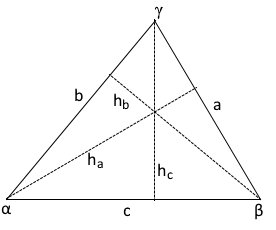
Important Note: Any of the three sides can be used as a base. The corresponding height, which is perpendicular to that base, must always be used. The graphic shows all three possible base-height combinations.
The Classic Triangle Area Formula in Theory and Practice
The classic area formula A = ½ × Base × Height is the most fundamental and intuitive method for calculating triangle areas. It is based on the basic geometric principle that a triangle is exactly half of a parallelogram with the same base and height.
Historical Development and Significance
The formula A = ½ × a × h belongs to the oldest mathematical insights of humanity:
- Ancient civilizations: Babylonians and Egyptians used this formula over 4000 years ago
- Practical application: For land surveying and construction planning in early civilizations
- Euclid's Elements: Systematic treatment and proof in Greek mathematics
- Modern relevance: Still the most important foundation for area calculations
Geometric Interpretation and Understanding
Parallelogram Relationship
A triangle is exactly half of a parallelogram with the same base and height. This fundamental relationship explains the factor ½ in the formula.
Rectangle Analogy
For right triangles, this relationship becomes particularly clear: the triangle is half of a rectangle.
Universal Validity
The formula works for all triangle types: acute, right, obtuse, isosceles, or irregular.
Height Concept
The height is always the shortest connection between a point and the opposite side - therefore always perpendicular.
Understanding the Height Concept
The height is one of the most important elements of triangle geometry:
- Definition: Perpendicular line from a vertex to the opposite side (or its extension)
- Three heights: Every triangle has exactly three heights - one to each side
- Orthocenter: All three heights intersect at one point (orthocenter)
- Position dependency: In acute triangles all heights lie inside, in obtuse triangles two lie outside
Practical Applications
The classic area formula finds wide application in many areas:
- Surveying: Property areas, triangulation, terrain surveying
- Construction: Roof areas, gables, structural elements
- Agriculture: Field areas, irrigation planning, yield calculation
- Architecture: Area division, space planning, material calculation
- Computer graphics: Polygon rendering, 3D modeling, area analysis
- Physics: Force diagrams, center of gravity calculations, moment calculation
Height Calculation Methods
The height can be determined in various ways:
Direct Measurement
- Physical measurement with tape measure or measuring instruments
- Perpendicular projection onto the base
- Use of right-angled aids
Mathematical Calculation
- Trigonometry: h = b × sin(α)
- Pythagoras: via right-angled sub-triangles
- Coordinate geometry: point-line distance formula
Advantages of the Classic Formula
- Intuitive: Geometrically very easy to understand and visualize
- Simplicity: Only two parameters required (base and height)
- Precision: Very accurate results with exact height measurement
- Universality: Works for all triangle shapes
- Foundation: Basis for many advanced geometric calculations
Comparison with Other Area Formulas
Classic Formula
A = ½ah
Advantage: Simple and intuitive
Disadvantage: Height measurement required
Heron's Formula
A = √[s(s-a)(s-b)(s-c)]
Advantage: Only side lengths
Disadvantage: More complex calculation
Sine Formula
A = ½ab sin(γ)
Advantage: Two sides + angle
Disadvantage: Trigonometry required
Error Sources and Accuracy
When applying the classic formula, various aspects must be considered:
- Height measurement: The height must be measured exactly perpendicular to the base
- Base choice: Any side can serve as base - important is the correct height
- External heights: In obtuse triangles some heights lie outside
- Units: Use consistent units for base and height
- Rounding errors: Sufficient decimal places for accurate results
Extensions and Generalizations
The principle of the classic area formula can be extended:
- Trapezoids: A = ½(a + c) × h (average of parallel sides × height)
- Polygons: Decomposition into triangles and application of the formula
- 3D geometry: Foundation for volume calculations of pyramids
- Integration: Generalization for curvilinearly bounded areas
Summary
The classic triangle area formula A = ½ × Base × Height is a fundamental tool of geometry that combines simplicity with universal applicability. Its geometric intuition and practical relevance make it an indispensable component of mathematical basic education and an important aid in many technical and scientific areas. Understanding height geometry and the various calculation possibilities opens the way to advanced geometric concepts.
|
|
Bisector of a triangle • Equilateral triangle • Right triangles • Right triangle, given 1 side and 1 angle • Isosceles right triangles • Isosceles triangles • Triangle area, given 2 sides and 1 anglee • Triangle area, given 1 side and 2 angles • Triangle, Incircle, given 3 sides • Area of a triangle given base and height • Triangle vertices, 3 x/y points •