Isosceles Right Triangle
45°-45°-90° Triangle: Symmetry and right angle in perfect combination
Isosceles Calculator
45°-45°-90° Triangle
An isosceles right triangle has a right angle (90°) and two 45° angles. Both legs are equal in length.
45°-45°-90° Triangle
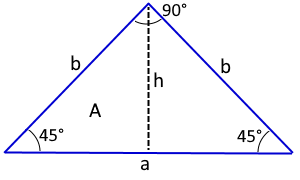
Isosceles right triangle with two equal legs.
The angles are 45°, 45°, and 90°.
Special Properties
Legs: Both equal length
Symmetry: Mirror axis through height
What is an Isosceles Right Triangle?
An isosceles right triangle combines two special properties:
- Right-angled: One angle is exactly 90°
- Isosceles: Two sides are equal in length (the legs)
- 45° angles: The two acute angles are each 45°
- Symmetry: Mirror axis through the height to the hypotenuse
- Ratio: Side ratio 1:1:√2
- Applications: Common in engineering and architecture
Symmetry and Equality
The symmetry gives this triangle special properties:
Equal Legs
- Both legs have identical length
- Form a right angle (90°)
- Stand perpendicular to each other
- Symmetric arrangement to the right angle
Mirror Axis
- Height to hypotenuse is axis of symmetry
- Divides the triangle into two congruent halves
- Bisects the hypotenuse at right angles
- Each half is a right triangle
The 45° Angles
The two 45° angles are the characteristic feature:
Angle Properties
- Both acute angles are identical (45°)
- Complement each other to the right angle (45° + 45° = 90°)
- Angle sum: 45° + 45° + 90° = 180°
- Complementary angles to each other
Trigonometric Values
- sin(45°) = cos(45°) = √2/2 ≈ 0.707
- tan(45°) = 1 (perfect symmetry)
- Unit circle: 45° = π/4 radians
- Exact values without approximations
Special Triangle in Mathematics
The 45°-45°-90° triangle is one of the most important triangles:
Side Ratio
Leg : Leg : Hypotenuse
Square Root of 2
Hypotenuse = Leg × √2
Simple Formulas
Height = half hypotenuse
Formulas for Isosceles Right Triangles
Basic Formulas
Leg: \( \ \displaystyle a = \frac{b}{\sqrt{2}}\)
Ratio 1:√2 between leg and hypotenuse
Height to Hypotenuse
Height is half of the base (hypotenuse)
Area
Quarter of the square of the hypotenuse
Perimeter
Hypotenuse times (1 + √2)
Alternative Formulas
\[a = b\sqrt{2}\], \[h = \frac{b\sqrt{2}}{2}\]
\[a = 2h\], \[b = h\sqrt{2}\]
\[a = 2\sqrt{A}\], \[b = \sqrt{2A}\]
\[b = \frac{a}{\sin(45°)} = \frac{a}{\cos(45°)}\]
Notation and Symbols
- a: Hypotenuse (base, longest side)
- b: Leg (both legs equal length)
- h: Height to hypotenuse
- A: Area
- U: Perimeter
- √2: Square root of 2 ≈ 1.414
- 45°: The two acute angles
- 90°: The right angle
Calculation Example
Given
Isosceles right triangle
1. Calculate Legs
Both legs are equal in length
2. Calculate Height
Height is half the hypotenuse
3. Calculate Area
Quarter of the hypotenuse square
4. Calculate Perimeter
Hypotenuse plus both legs
Verification
- Pythagoras: (5√2)² + (5√2)² = 50 + 50 = 100 = 10² ✓
- Angles: 45° + 45° + 90° = 180° ✓
- Ratio: 7.07:7.07:10 ≈ 1:1:√2 ✓
The Isosceles Right Triangle in Mathematics and Practice
The isosceles right triangle (also called 45°-45°-90° triangle) is one of the most important special triangles in mathematics. It combines the properties of a right triangle with the symmetry of an isosceles triangle, thus forming a perfect bridge between geometry, algebra, and practical applications.
Geometric Properties and Symmetry
The special combination of right angle and isosceles nature gives this triangle unique properties:
- Double symmetry: Both point and axis symmetric with respect to the height to the hypotenuse
- Perfect angle distribution: 45°-45°-90° creates a harmonious division
- Congruent halves: The height divides the triangle into two identical right triangles
- Isometric legs: Both legs have exactly the same length
- Optimal proportions: The side ratio 1:1:√2 is mathematically elegant
The Ratio 1:1:√2 and Its Significance
The characteristic side ratio has deep mathematical meaning:
Mathematical Elegance
The square root of 2 (√2 ≈ 1.414) occurs naturally when a square is divided diagonally into two triangles.
Pythagorean Theorem
Perfect demonstration: a² + a² = (a√2)², shows the application of the Pythagorean theorem in pure form.
Geometric Construction
Easy to construct: divide a square diagonally or modify an equilateral triangle.
Irrational Number
√2 is the first historically known irrational number, discovered by the Pythagoreans.
Trigonometric Peculiarities
The 45° angles yield special trigonometric values:
Exact Values
- sin(45°) = cos(45°) = √2/2 ≈ 0.7071
- tan(45°) = 1 (perfect symmetry)
- No approximations needed: algebraically exact
- Unit circle: 45° = π/4 radians
Functional Relationships
- sin(45°) = cos(45°): perfect symmetry
- tan(45°) = 1: slope of 45° is 1:1
- Complementary equality at 45°
- Foundation for trigonometric identities
Practical Applications
The 45°-45°-90° triangle is ubiquitous in practice:
Architecture and Construction
- Roof slopes: 45° for optimal drainage
- Stairs: standard slope for comfort
- Corner connections: miter cuts at 45°
- Foundation trenches: slope angles
Design and Art
- Diagonal compositions
- Golden ratio derivatives
- Symmetric designs
- Optical balance
Technology and Engineering
- Mechanical engineering: chamfers and edges
- Optics: beam splitting at 45°
- Electronics: crystal structures
- Navigation: course calculations
Computer Science and Graphics
- Pixel grids: diagonal lines
- 3D graphics: standard rotations
- Image processing: edge filters
- Game development: movement directions
Historical and Cultural Significance
Ancient Mathematics
The Babylonians and Egyptians already used 45° triangles for constructions and discovered that the diagonal of a square is incommensurable to its side.
Pythagorean School
The discovery of the irrationality of √2 from the isosceles right triangle led to the first crisis in Greek mathematics.
Buddhist Culture
In Buddhist architecture, the 45° angle symbolizes the balance between heaven and earth.
Modern Mathematics
Foundation for complex numbers, rotations in the plane, and Fourier analysis.
Construction and Drawing
The isosceles right triangle can be constructed in various ways:
- From the square: Diagonal divides square into two congruent triangles
- With compass and straightedge: Right angle + equal legs
- Via 45° angle: Angle bisection of the right angle
- Coordinate geometry: Connect points (0,0), (a,0), (0,a)
- Folding technique (Origami): Fold square diagonally
Generalizations and Extensions
Higher Dimensions
In 3D it corresponds to half the diagonal of a cube, in n-dimensional spaces similar relationships arise.
Fractal Geometry
Sierpinski triangle and other fractals use the self-similarity of the 45°-45°-90° triangle.
Complex Numbers
The 45° rotation corresponds to multiplication by (1+i)/√2 in the complex plane.
Crystallography
Cubic crystal systems frequently show 45° angles in their cleavage planes.
Educational Significance
In mathematics education, the isosceles right triangle is of particular importance:
- Introduction to irrational numbers: √2 as the first example
- Understanding Pythagoras: Intuitive demonstration of the theorem
- Trigonometry basics: Exact values without calculator
- Symmetry concepts: Multiple symmetry properties
- Construction exercises: Simple and elegant constructions
Summary
The isosceles right triangle is a masterpiece of geometric elegance. It connects fundamental mathematical concepts like irrational numbers, trigonometric functions, and symmetry in a single, simple form. Its practical relevance ranges from ancient architecture to modern computer graphics and makes it one of the most important special triangles in mathematics.
|
|
Bisector of a triangle • Equilateral triangle • Right triangles • Right triangle, given 1 side and 1 angle • Isosceles right triangles • Isosceles triangles • Triangle area, given 2 sides and 1 anglee • Triangle area, given 1 side and 2 angles • Triangle, Incircle, given 3 sides • Area of a triangle given base and height • Triangle vertices, 3 x/y points •