Calculate Isosceles Triangle
Online calculator and formulas for calculating an isosceles triangle
Isosceles Triangle Calculator
Symmetric Triangle
An isosceles triangle has two equal sides (legs) and a line of symmetry through the apex.
Visualization
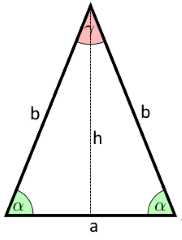
The diagram shows an isosceles triangle with base a and legs b.
The height h divides the triangle into two congruent right triangles.
What is an Isosceles Triangle?
An isosceles triangle is a triangle with special symmetry properties:
- Two equal sides: The legs b have the same length
- Base: The third side a is the baseline
- Line of symmetry: The height h divides the triangle symmetrically
- Equal base angles: The angles at the base are identical
- Application: Architecture, roof constructions, design
- Calculation: All other values derivable from two parameters
Symmetry and Special Properties
The symmetry gives the isosceles triangle special properties:
Line of Symmetry
- The height h is the line of symmetry
- Divides the base a into two equal halves
- Stands perpendicular to the base
- Divides the triangle into two congruent parts
Angle Properties
- Two base angles are equal (both α)
- Apex angle γ = 180° - 2α
- Symmetric arrangement
- Simple relationships between each other
How Does the Calculation Work?
The calculator requires two parameters for a complete calculation:
Possible Parameters
- Base a: The base side of the triangle
- Leg b: One of the two equal sides
- Height h: Perpendicular from apex to base
- Area A: The area content
- Angle α: A base angle
Calculation Logic
- At least one side length required
- Use symmetry properties
- Apply trigonometric relationships
- All parameters derivable from two values
Formulas for Isosceles Triangle
Base a
Base from leg and base angle
Leg b
Leg from base and angle
Height h
Height from leg and base angle
Area A
Standard triangle formula
Perimeter U
Base plus two equal legs
Base Angle α
Angle from height and base
Additional Important Formulas
Symbols and Notation
- a: Base (base side) of the triangle
- b: Leg (the two equal sides)
- h: Height (from apex to base)
- A: Area of the triangle
- U: Perimeter of the triangle
- α: Base angle (both equal)
- γ: Apex angle (at the top)
- °: Degree (angle measure)
Calculation Example
Given
1. Calculate Height
Pythagorean theorem in half triangle
2. Calculate Area
Standard triangle formula
3. Calculate Perimeter
Base plus twice the leg
4. Calculate Base Angle
Apex angle γ = 180° - 2 × 65.4° = 49.2°
The Isosceles Triangle in Mathematics and Practice
The isosceles triangle is one of the most fundamental shapes in geometry and combines simplicity with elegantly symmetric properties. It is the perfect example of how a single condition (two equal sides) leads to a multitude of interesting mathematical relationships.
Definition and Basic Properties
An isosceles triangle is defined by:
- Two equal sides: The so-called legs (both with length b)
- One base: The third side (length a), usually shown horizontally
- Line of symmetry: The height from apex to base divides the triangle symmetrically
- Equal base angles: The two angles at the base are identical
Symmetry Properties
Symmetry is the characteristic feature of the isosceles triangle:
Axial Symmetry
The height h is simultaneously the line of symmetry, perpendicular bisector of the base, and angle bisector of the apex angle.
Congruent Division
The line of symmetry divides the triangle into two congruent right triangles.
Angle Symmetry
The two base angles α are always equal, regardless of the side lengths.
Special Points
Center of gravity, circumcenter, and other special points lie on the line of symmetry.
Practical Applications
Isosceles triangles are ubiquitous in nature, technology, and art:
- Architecture: Gables, roofs, Gothic arches, modern bridge constructions
- Nature: Crystal structures, leaf shapes, mountain peak profiles
- Technology: Truss beams, bracing, antenna structures
- Design: Logos, arrows, direction indicators, warning signs
- Musical instruments: Harps, triangles, bell shapes
- Navigation: Triangulation, bearing, GPS calculations
Mathematical Relationships
Trigonometric Relationships
Symmetry enables simple trigonometric calculations. The height divides the triangle into two right triangles.
Pythagorean Theorem Applicable
In the two right halves: h² + (a/2)² = b²
Angle Relationships
The sum of angles is 180°: 2α + γ = 180°, therefore γ = 180° - 2α
Special Cases
Becomes equilateral when a = b, right-angled when γ = 90°
Construction Methods
An isosceles triangle can be constructed in various ways:
- Compass method: Draw base, strike circles with radius b from endpoints
- Symmetry method: Construct perpendicular bisector of base, mark off leg length
- Angle method: Construct base angle α and draw legs accordingly
- Height method: Construct height h and draw legs from there to base
Special Properties and Theorems
Special geometric theorems apply to isosceles triangles:
- Base angle theorem: In an isosceles triangle, the base angles are equal
- Converse: If two angles are equal, the triangle is isosceles
- Line of symmetry property: Height, perpendicular bisector of base, angle bisector, and median coincide
- Circumcircle property: The circumcenter lies on the line of symmetry
- Incircle property: The incenter also lies on the line of symmetry
Historical and Cultural Significance
The isosceles triangle has a rich history in various cultures:
- Ancient geometry: Already extensively treated and classified by Euclid
- Architectural history: From Egyptian pyramids to modern skyscrapers
- Symbolism: Represents stability, aspiration, direction, and purposefulness
- Art and design: Basic form for countless artistic and design works
- Mathematical development: Important building block for the development of trigonometry
Related Triangle Forms
The isosceles triangle is related to other special triangles:
- Equilateral triangle: Special case with a = b (all sides equal)
- Right triangle: Can be isosceles (45°-45°-90° triangle)
- Acute triangle: All angles < 90°, often isosceles
- Obtuse triangle: One angle > 90°, can be isosceles
Summary
The isosceles triangle is a perfect example of the elegance of geometry. A simple condition (two equal sides) leads to a wealth of mathematical properties, practical applications, and aesthetic qualities. It connects simplicity with symmetry and is therefore of great importance in both pure mathematics and applied science.
|
|
Bisector of a triangle • Equilateral triangle • Right triangles • Right triangle, given 1 side and 1 angle • Isosceles right triangles • Isosceles triangles • Triangle area, given 2 sides and 1 anglee • Triangle area, given 1 side and 2 angles • Triangle, Incircle, given 3 sides • Area of a triangle given base and height • Triangle vertices, 3 x/y points •