Gleichschenkliges Dreieck berechnen

Online Rechner und Formeln zur Berechnung eines gleichschenkligen Dreiecks

Gleichschenkliges Dreieck Rechner

Symmetrisches Dreieck

Ein gleichschenkliges Dreieck hat zwei gleich lange Seiten (Schenkel) und eine Symmetrieachse durch die Spitze.

Gegebene Parameter auswählen

Erster Parameter

Zweiter Parameter

Wert 1

Wert für den ersten Parameter

Wert 2

Wert für den zweiten Parameter

Dezimalstellen

Ergebnisse

Basis a:

Seite b:

Höhe h:

Umfang P:

Fläche A:

Winkel α:

Winkel γ:

Visualisierung

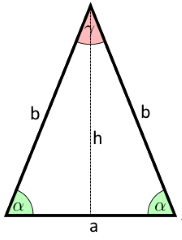
Das Diagramm zeigt ein gleichschenkliges Dreieck mit Basis a und Schenkeln b.
Die Höhe h teilt das Dreieck in zwei kongruente rechtwinklige Dreiecke.

Was ist ein gleichschenkliges Dreieck?

Ein gleichschenkliges Dreieck ist ein Dreieck mit besonderen Symmetrieeigenschaften:

Zwei gleiche Seiten: Die Schenkel b haben die gleiche Länge
Basis: Die dritte Seite a ist die Grundlinie
Symmetrieachse: Die Höhe h teilt das Dreieck symmetrisch

Gleiche Basiswinkel: Die Winkel an der Basis sind identisch
Anwendung: Architektur, Dachkonstruktionen, Design
Berechnung: Aus zwei Parametern alle anderen ableitbar

Symmetrie und besondere Eigenschaften

Die Symmetrie verleiht dem gleichschenkligen Dreieck besondere Eigenschaften:

Symmetrieachse

Die Höhe h ist die Symmetrieachse
Teilt die Basis a in zwei gleiche Hälften
Steht senkrecht auf der Basis
Teilt das Dreieck in zwei kongruente Teile

Winkel-Eigenschaften

Zwei Basiswinkel sind gleich (beide α)
Spitzenwinkel γ = 180° - 2α
Symmetrische Anordnung
Einfache Beziehungen untereinander

Wie funktioniert die Berechnung?

Der Rechner benötigt zwei Parameter für eine vollständige Berechnung:

Mögliche Parameter

Basis a: Die Grundseite des Dreiecks
Schenkel b: Eine der beiden gleichen Seiten
Höhe h: Senkrechte von der Spitze zur Basis
Fläche A: Der Flächeninhalt
Winkel α: Ein Basiswinkel

Berechnungslogik

Mindestens eine Seitenlänge erforderlich
Symmetrie-Eigenschaften nutzen
Trigonometrische Beziehungen anwenden
Alle Parameter aus zwei Werten ableitbar

Formeln zum gleichschenkligen Dreieck

Basis a

\[a = 2 \cdot b \cdot \cos(\alpha)\]

Basis aus Schenkel und Basiswinkel

Schenkel b

\[b = \frac{a}{2 \cdot \cos(\alpha)}\]

Schenkel aus Basis und Winkel

Höhe h

\[h = b \cdot \sin(\alpha)\]

Höhe aus Schenkel und Basiswinkel

Fläche A

\[A = \frac{a \cdot h}{2}\]

Standard-Dreiecksformel

Umfang U

\[U = a + 2 \cdot b\]

Basis plus zwei gleiche Schenkel

Basiswinkel α

\[\alpha = \arctan\left(\frac{2h}{a}\right)\]

Winkel aus Höhe und Basis

Weitere wichtige Formeln

Höhe aus Schenkel: \(h = \sqrt{b^2 - \frac{a^2}{4}}\)

Spitzenwinkel: \(\gamma = 180° - 2\alpha\)

Fläche alternativ: \(A = \frac{b^2 \sin(2\alpha)}{2}\)

Schenkel aus Höhe: \(b = \frac{h}{\sin(\alpha)}\)

Symbole und Bezeichnungen

a: Basis (Grundseite) des Dreiecks
b: Schenkel (die beiden gleichen Seiten)
h: Höhe (von der Spitze zur Basis)
A: Flächeninhalt des Dreiecks

U: Umfang des Dreiecks
α: Basiswinkel (beide gleich)
γ: Spitzenwinkel (an der Spitze)
°: Grad (Winkelmaß)

Rechenbeispiel

Gegeben

Basis a = 5 Schenkel b = 6

1. Höhe berechnen

\[h = \sqrt{6^2 - \frac{5^2}{4}} = \sqrt{36 - 6.25} \approx 5.45\]

Pythagoras im halben Dreieck

2. Fläche berechnen

\[A = \frac{5 \times 5.45}{2} \approx 13.63\]

Standard-Dreiecksformel

3. Umfang berechnen

\[U = 5 + 2 \times 6 = 17\]

Basis plus zweimal Schenkel

4. Basiswinkel berechnen

\[\alpha = \arctan\left(\frac{2 \times 5.45}{5}\right) \approx 65.4°\]

Spitzenwinkel γ = 180° - 2 × 65.4° = 49.2°

Das gleichschenklige Dreieck in Mathematik und Praxis

Das gleichschenklige Dreieck ist eine der fundamentalsten Formen in der Geometrie und vereint Einfachheit mit elegant symmetrischen Eigenschaften. Es ist das perfekte Beispiel dafür, wie eine einzige Bedingung (zwei gleiche Seiten) zu einer Vielzahl interessanter mathematischer Beziehungen führt.

Definition und Grundeigenschaften

Ein gleichschenkliges Dreieck ist definiert durch:

Zwei gleiche Seiten: Die sogenannten Schenkel (beide mit Länge b)
Eine Basis: Die dritte Seite (Länge a), die meist horizontal dargestellt wird
Symmetrieachse: Die Höhe von der Spitze zur Basis teilt das Dreieck symmetrisch
Gleiche Basiswinkel: Die beiden Winkel an der Basis sind identisch

Symmetrie-Eigenschaften

Die Symmetrie ist das charakteristische Merkmal des gleichschenkligen Dreiecks:

Achsensymmetrie

Die Höhe h ist gleichzeitig Symmetrieachse, Mittelsenkrechte der Basis und Winkelhalbierende des Spitzenwinkels.

Kongruente Teilung

Die Symmetrieachse teilt das Dreieck in zwei kongruente rechtwinklige Dreiecke.

Winkel-Symmetrie

Die beiden Basiswinkel α sind immer gleich, unabhängig von den Seitenlängen.

Besondere Punkte

Schwerpunkt, Umkreismittelpunkt und andere besondere Punkte liegen auf der Symmetrieachse.

Praktische Anwendungen

Gleichschenklige Dreiecke sind allgegenwärtig in Natur, Technik und Kunst:

Architektur: Giebel, Dächer, gotische Bögen, moderne Brückenkonstruktionen
Natur: Kristallstrukturen, Blattformen, Berggipfel-Profile
Technik: Fachwerkträger, Verstrebungen, Antennenstrukturen
Design: Logos, Pfeile, Richtungsanzeiger, Warnschilder
Musikinstrumente: Harfen, Triangel, Glockenformen
Navigation: Triangulation, Peilung, GPS-Berechnungen

Mathematische Beziehungen

Trigonometrische Beziehungen

Die Symmetrie ermöglicht einfache trigonometrische Berechnungen. Die Höhe teilt das Dreieck in zwei rechtwinklige Dreiecke.

Pythagoras anwendbar

In den beiden rechtwinkligen Hälften gilt: h² + (a/2)² = b²

Winkelbeziehungen

Die Summe der Winkel beträgt 180°: 2α + γ = 180°, daher γ = 180° - 2α

Spezialfälle

Wird zum gleichseitigen Dreieck wenn a = b, zum rechtwinkligen wenn γ = 90°

Konstruktionsmethoden

Ein gleichschenkliges Dreieck kann auf verschiedene Weise konstruiert werden:

Zirkel-Methode: Basis zeichnen, von den Endpunkten Kreise mit Radius b schlagen
Symmetrie-Methode: Mittelsenkrechte der Basis errichten, Schenkel-Länge abtragen
Winkel-Methode: Basiswinkel α konstruieren und Schenkel entsprechend zeichnen
Höhen-Methode: Höhe h konstruieren und von dort aus die Schenkel zur Basis

Besondere Eigenschaften und Sätze

Für gleichschenklige Dreiecke gelten spezielle geometrische Sätze:

Basiswinkelsatz: In einem gleichschenkligen Dreieck sind die Basiswinkel gleich
Umkehrung: Sind zwei Winkel gleich, ist das Dreieck gleichschenklig
Symmetrieachsen-Eigenschaft: Höhe, Mittelsenkrechte der Basis, Winkelhalbierende und Seitenhalbierende fallen zusammen
Umkreis-Eigenschaft: Der Umkreismittelpunkt liegt auf der Symmetrieachse
Inkreis-Eigenschaft: Der Inkreismittelpunkt liegt ebenfalls auf der Symmetrieachse

Historische und kulturelle Bedeutung

Das gleichschenklige Dreieck hat eine reiche Geschichte in verschiedenen Kulturen:

Antike Geometrie: Bereits von Euklid ausführlich behandelt und klassifiziert
Architektur-Geschichte: Von ägyptischen Pyramiden bis zu modernen Wolkenkratzern
Symbolik: Steht für Stabilität, Aufstreben, Richtung und Zielgerichtetheit
Kunst und Design: Grundform für unzählige künstlerische und gestalterische Arbeiten
Mathematische Entwicklung: Wichtiger Baustein für die Entwicklung der Trigonometrie

Weitere Dreieck Funktionen

Gleichschenkliges Dreieck • Gleichseitiges Dreieck • Flächeninhalt Basis, 2 Winkel • Flächeninhalt 2 Seiten, 1 Winkel • Flächeninhalt aus 3 Seiten • Flächeninhalt aus Basis, Höhe • Rechtwinkliges Dreieck 1 Seite, 1 Winkel • Rechtwinkliges Dreieck 2 Seiten • Rechtwinkliges, gleichschenkliges Dreieck • Seitenhalbierende • Innenkreis • Dreieck im Koordinatensystem •