Seitenhalbierende berechnen
Berechnung der Mediane und des Schwerpunkts eines Dreiecks
Seitenhalbierende Rechner
Mediane und Schwerpunkt
Seitenhalbierende (Mediane) verbinden Eckpunkte mit Seitenmittelpunkten. Ihr Schnittpunkt (Schwerpunkt) ist der Gleichgewichtspunkt des Dreiecks.
Mediane im Dreieck
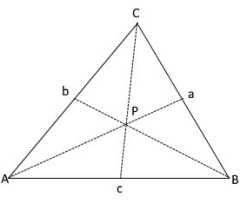
Die drei Mediane (rot) verbinden Eckpunkte mit Seitenmittelpunkten.
Der Schwerpunkt P teilt jede Seitenhalbierende im Verhältnis 2:1.
Was sind Seitenhalbierende?
Seitenhalbierende (Mediane) sind fundamentale Linien in jedem Dreieck:
- Definition: Verbindet Eckpunkt mit Mittelpunkt der gegenüberliegenden Seite
- Anzahl: Jedes Dreieck hat genau drei Mediane
- Teilung: Jede Seitenhalbierende teilt das Dreieck in zwei flächengleiche Teile
- Schnittpunkt: Alle drei Mediane treffen sich im Schwerpunkt
- Verhältnis: Schwerpunkt teilt jede Median im Verhältnis 2:1
- Gleichgewicht: Der Schwerpunkt ist der Balancepunkt des Dreiecks
Der Schwerpunkt (Zentroid)
Der Schwerpunkt ist der bemerkenswerte Schnittpunkt aller drei Mediane:
Eindeutiger Schnittpunkt
- Alle drei Mediane treffen sich in einem Punkt
- Liegt immer im Inneren des Dreiecks
- Unabhängig von der Dreiecksform
- Geometrisches Zentrum des Dreiecks
2:1 Teilungsverhältnis
- Teilt jede Median in zwei Abschnitte
- Vom Eckpunkt: 2/3 der Medianlänge
- Zur gegenüberliegenden Seite: 1/3 der Medianlänge
- Konstantes Verhältnis bei allen Dreiecken
Gleichgewicht und physikalische Eigenschaften
Der Schwerpunkt hat besondere physikalische Bedeutung:
Balancepunkt
- Dreieck balanciert perfekt auf diesem Punkt
- Massenschwerpunkt bei homogener Dichte
- Gleichgewicht in alle Richtungen
- Minimaler Trägheitsmoment-Punkt
Flächenteilung
- Jede Median teilt Dreieck in zwei gleiche Flächen
- Schwerpunkt teilt Dreieck in drei gleiche Teilflächen
- Alle Teilung durch Schwerpunkt sind flächengleich
- Optimale Aufteilung für viele Anwendungen
Besondere Eigenschaften der Mediane
Mediane haben einzigartige mathematische Eigenschaften:
Flächenteilung
- Teilt Dreieck in zwei flächengleiche Teile
- Beide Teilflächen = A/2
- Unabhängig von Dreiecksform
Längenbeziehung
- Länge abhängig von allen drei Seiten
- Apollonius-Theorem anwendbar
- Verbindung zu Seitenlängen
Schwerpunkt
- Immer im Dreiecksinneren
- 2:1 Teilungsverhältnis konstant
- Koordinaten = Mittelwert der Eckpunkte
Formeln für Seitenhalbierende
Median mₐ (von A)
Median vom Eckpunkt A zur Seite a
Median m_b (von B)
Median vom Eckpunkt B zur Seite b
Median m_c (von C)
Median vom Eckpunkt C zur Seite c
Apollonius-Theorem
Die Formeln für Mediane basieren auf dem Apollonius-Theorem, das die Beziehung zwischen Seitenlängen und Medianen beschreibt:
Dieses Theorem zeigt, wie die Länge einer Median von allen drei Seitenlängen abhängt.
Schwerpunkt-Koordinaten
Wenn die Eckpunkte bekannt sind: A(x₁,y₁), B(x₂,y₂), C(x₃,y₃), dann sind die Schwerpunkt-Koordinaten:
Der Schwerpunkt ist der Mittelwert aller Eckpunkt-Koordinaten.
Bezeichnungen und Symbole
- a, b, c: Seitenlängen des Dreiecks
- mₐ, m_b, m_c: Mediane (Seitenhalbierende)
- S (oder G): Schwerpunkt (Zentroid)
- A, B, C: Eckpunkte des Dreiecks
- 2:1: Teilungsverhältnis am Schwerpunkt
- Mₐ, M_b, M_c: Seitenmittelpunkte
- Median: Englisch für Seitenhalbierende
- Zentroid: Anderer Name für Schwerpunkt
Rechenbeispiel
Gegeben
Rechtwinkliges Dreieck (3-4-5)
1. Median mₐ berechnen
Median von A zur Seite a
2. Median m_b berechnen
Median von B zur Seite b
3. Median m_c berechnen
Median von C zur Hypotenuse
Besonderheit
Im rechtwinkligen Dreieck ist die Median zur Hypotenuse genau halb so lang wie die Hypotenuse selbst: m_c = c/2 = 5/2 = 2.5 ✓
Seitenhalbierende in Mathematik und Anwendung
Seitenhalbierende (Mediane) gehören zu den fundamentalsten Linien der Dreiecksgeometrie. Sie verbinden geometrische Eleganz mit praktischer Anwendbarkeit und zeigen bemerkenswerte mathematische Eigenschaften, die weit über die reine Geometrie hinausreichen.
Definition und Grundeigenschaften
Eine Seitenhalbierende ist definiert als die Verbindungslinie zwischen einem Eckpunkt und dem Mittelpunkt der gegenüberliegenden Seite:
- Eindeutige Definition: Jeder Eckpunkt bestimmt genau eine Seitenhalbierende
- Drei Mediane: Jedes Dreieck hat exakt drei Seitenhalbierende
- Flächenteilung: Jede Median teilt das Dreieck in zwei flächengleiche Hälften
- Innere Lage: Mediane verlaufen immer vollständig im Dreieckinneren
- Universalität: Existieren in jedem Dreieck, unabhängig von Form oder Größe
Der Schwerpunkt - Ein besonderer Punkt
Der Schnittpunkt aller drei Mediane hat außergewöhnliche Eigenschaften:
Geometrische Eigenschaften
Der Schwerpunkt liegt immer im Inneren des Dreiecks und teilt jede Median im Verhältnis 2:1, wobei der längere Abschnitt zum Eckpunkt zeigt.
Koordinatenberechnung
Die Koordinaten des Schwerpunkts sind einfach das arithmetische Mittel der Eckpunkt-Koordinaten.
Physikalische Bedeutung
Bei homogener Massenverteilung ist der Schwerpunkt der Massenschwerpunkt und Gleichgewichtspunkt des Dreiecks.
Minimaleigenschaft
Der Schwerpunkt minimiert die Summe der quadrierten Abstände zu allen Eckpunkten.
Das Apollonius-Theorem
Die Längen der Mediane werden durch das elegante Apollonius-Theorem beschrieben:
Mathematische Formulierung
Für die Median mₐ gilt: 4m²ₐ = 2b² + 2c² - a². Diese Beziehung verbindet alle Seitenlängen mit der Medianlänge.
Herleitung
Das Theorem lässt sich elegant über Vektorrechnung oder den Cosinussatz herleiten.
Anwendung
Ermöglicht die direkte Berechnung von Medianlängen aus den drei Seitenlängen ohne Winkelberechnungen.
Verallgemeinerung
Das Theorem kann auf höhere Dimensionen und andere geometrische Objekte erweitert werden.
Praktische Anwendungen
Seitenhalbierende und der Schwerpunkt haben vielfältige praktische Anwendungen:
- Ingenieurswesen: Schwerpunktbestimmung für Belastungsberechnungen, Tragwerksplanung
- Computergrafik: Triangulation, Mesh-Generierung, Schwerpunkt-basierte Algorithmen
- Robotik: Gleichgewichtssteuerung, Pfadplanung, Massenschwerpunkt-Berechnung
- Physik: Rotationsdynamik, Trägheitsmomente, Stabilität bewegter Objekte
- Kartographie: Flächenschwerpunkte von Regionen, geografische Zentren
- Architektur: Statische Berechnungen, Materialverteilung, Gewichtsbalance
Beziehungen zu anderen Dreieckslinien
Höhen
Im Gegensatz zu Höhen stehen Mediane nicht senkrecht auf den Seiten, haben aber andere bemerkenswerte Eigenschaften.
Winkelhalbierende
Nur im gleichseitigen Dreieck fallen Mediane und Winkelhalbierende zusammen.
Mittelsenkrechte
Mittelsenkrechte und Mediane sind völlig verschiedene Linien mit unterschiedlichen Eigenschaften.
Seitenhalbierende der Mittellinien
Die Verbindungslinien der Seitenmittelpunkte bilden das Mitteldreieck mit besonderen Eigenschaften.
Spezialfälle und besondere Dreiecke
In verschiedenen Dreieckstypen zeigen Mediane spezielle Eigenschaften:
- Gleichseitiges Dreieck: Alle Mediane sind gleich lang und fallen mit Höhen, Winkelhalbierenden und Mittelsenkrechten zusammen
- Gleichschenkliges Dreieck: Die Median zur Basis fällt mit der Höhe zusammen
- Rechtwinkliges Dreieck: Die Median zur Hypotenuse ist genau halb so lang wie die Hypotenuse
- Stumpfwinkliges Dreieck: Alle Mediane bleiben im Dreieckinneren, obwohl eine Höhe außerhalb liegt
Historische Entwicklung
Die Erforschung der Mediane hat eine lange Geschichte:
Antike
Bereits in der griechischen Antike waren die Grundeigenschaften der Mediane bekannt.
Apollonius von Perga
Entwickelte um 200 v. Chr. das nach ihm benannte Theorem über Medianlängen.
Moderne Mathematik
Vektorielle und analytische Behandlung ermöglichten tiefere Einsichten in die Eigenschaften.
Anwendungsgebiete
Entwicklung neuer Anwendungen in Computerwissenschaft, Physik und Ingenieurswesen.
Algorithmen und Berechnung
Die Berechnung von Mediane erfolgt systematisch:
- Eingabe: Die drei Seitenlängen a, b, c des Dreiecks
- Validierung: Prüfung der Dreiecksungleichung
- Anwendung des Apollonius-Theorems: Für jede der drei Mediane
- Numerische Stabilität: Behandlung von Rundungsfehlern bei extremen Verhältnissen
- Ausgabe: Die drei Medianlängen mit gewünschter Genauigkeit
Zusammenfassung
Seitenhalbierende sind fundamentale geometrische Elemente, die elegante mathematische Eigenschaften mit praktischer Anwendbarkeit verbinden. Der Schwerpunkt als ihr gemeinsamer Schnittpunkt ist ein Punkt von außergewöhnlicher geometrischer und physikalischer Bedeutung. Das Apollonius-Theorem bietet eine elegante Methode zur Berechnung der Medianlängen und zeigt die tiefe Verbindung zwischen verschiedenen geometrischen Eigenschaften eines Dreiecks.
|
|