Dreieck Innenkreis berechnen
Berechnung mit Heron-Formel: Innenkreis, Fläche und Winkel aus drei Seitenlängen
Innenkreis Rechner
Innenkreis und Heron-Formel
Der Innenkreis berührt alle drei Seiten des Dreiecks. Mit der Heron-Formel werden Fläche und Inkreisradius aus den Seitenlängen berechnet.
Innenkreis Visualisierung
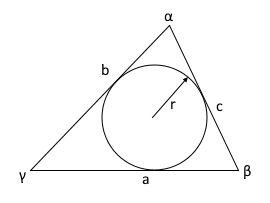
Der Innenkreis (blau) berührt alle drei Seiten des Dreiecks von innen.
Sein Mittelpunkt ist der Schnittpunkt der Winkelhalbierenden.
Was ist der Innenkreis eines Dreiecks?
Der Innenkreis (Inkreis) ist der größte Kreis, der vollständig im Dreieck liegt:
- Tangenten: Berührt alle drei Seiten des Dreiecks von innen
- Mittelpunkt: Schnittpunkt der drei Winkelhalbierenden (Inzentrum)
- Eindeutigkeit: Jedes Dreieck hat genau einen Innenkreis
- Maximaler Radius: Größter Kreis, der ins Dreieck passt
- Berechnung: Radius über Heron-Formel ermittelbar
- Anwendung: Optimierung, Materialverwendung, Geometrie
Die Heron-Formel
Die Heron-Formel ist ein eleganter Weg, die Dreiecksfläche aus den Seitenlängen zu berechnen:
Heron-Formel
Wobei s = (a+b+c)/2 der halbe Umfang ist
Inkreisradius
Radius aus Fläche und halbem Umfang
Tangenteneigenschaften
Der Innenkreis berührt die Dreiecksseiten als Tangenten:
Berührungspunkte
- Genau ein Berührungspunkt pro Seite
- Senkrechte vom Kreismittelpunkt zur Seite
- Abstand = Inkreisradius
- Symmetrische Anordnung
Tangentenlängen
- Von jedem Eckpunkt gleiche Tangentenlängen
- Aufteitung der Seiten in charakteristische Abschnitte
- Verbindung zum Umfang und zur Fläche
- Grundlage für weitere Berechnungen
Berechnungsalgorithmus
Der Rechner verwendet einen systematischen Ansatz basierend auf der Heron-Formel:
Schritt 1
Halber Umfang s = (a+b+c)/2 berechnen
Schritt 2
Fläche mit Heron-Formel ermitteln
Schritt 3
Inkreisradius r = A/s berechnen
Schritt 4
Winkel mit Cosinussatz bestimmen
Formeln für Innenkreis und Dreieck
Heron-Formel (Fläche)
Mit s = (a+b+c)/2
Inkreisradius
Fläche geteilt durch halben Umfang
Inkreisfläche
Standard-Kreisflächenformel
Alternative Heron-Formel
Symmetrische Darstellung
Winkelformeln (Cosinussatz)
\[\alpha = \arccos\left(\frac{b^2+c^2-a^2}{2bc}\right)\]
\[\beta = \arccos\left(\frac{a^2+c^2-b^2}{2ac}\right)\]
\[\gamma = \arccos\left(\frac{a^2+b^2-c^2}{2ab}\right)\]
Weitere Formeln
Bezeichnungen und Symbole
- a, b, c: Seitenlängen des Dreiecks
- A: Flächeninhalt des Dreiecks
- s: Halber Umfang (Semiperimeter)
- r: Inkreisradius
- α, β, γ: Innenwinkel des Dreiecks
- h: Höhe des Dreiecks
- π: Kreiszahl Pi (≈ 3.14159)
- °: Grad (Winkelmaß)
Rechenbeispiel
Gegeben
Rechtwinkliges Dreieck (5-4-3)
1. Halber Umfang
Basis für Heron-Formel
3. Inkreisradius
Fläche durch halben Umfang
2. Fläche (Heron)
Elegant mit Heron-Formel
4. Inkreisfläche
Standard-Kreisformel
Besonderheit
Im rechtwinkligen Dreieck gilt: r = (a+b-c)/2. Hier: r = (4+3-5)/2 = 1 ✓
Innenkreis und Heron-Formel in der Mathematik
Der Innenkreis eines Dreiecks und die Heron-Formel gehören zu den elegantesten Konzepten der Geometrie. Sie verbinden verschiedene Aspekte der Dreiecksgeometrie und zeigen die tiefe Verbindung zwischen Fläche, Umfang und den eingeschriebenen Kreisen.
Der Innenkreis - Definition und Eigenschaften
Der Innenkreis ist der eindeutig bestimmte Kreis, der alle drei Seiten des Dreiecks von innen berührt:
- Eindeutigkeit: Jedes Dreieck hat genau einen Innenkreis
- Mittelpunkt (Inzentrum): Schnittpunkt der drei Winkelhalbierenden
- Tangenteneigenschaft: Berührt alle drei Seiten als Tangenten
- Maximaler Radius: Größter Kreis, der vollständig ins Dreieck passt
- Symmetrie: Abstand vom Mittelpunkt zu allen drei Seiten ist gleich (= Radius)
Die Heron-Formel - Historischer Hintergrund
Die nach dem griechischen Mathematiker Heron von Alexandria benannte Formel ist ein Meisterwerk der antiken Geometrie:
Historische Entwicklung
Heron von Alexandria (ca. 10-70 n. Chr.) systematisierte diese Formel, obwohl sie möglicherweise schon früher bekannt war.
Mathematische Eleganz
Die Formel benötigt nur die drei Seitenlängen - keine Winkel oder Höhen müssen bekannt sein.
Praktische Bedeutung
Ermöglicht Flächenberechnungen in der Praxis, wo nur Seitenlängen messbar sind.
Moderne Anwendungen
Grundlage für Algorithmen in Computergrafik, Vermessung und numerischer Geometrie.
Verbindung zwischen Innenkreis und Heron-Formel
Die Beziehung r = A/s verbindet elegant den Inkreisradius mit der Dreiecksfläche:
Geometrische Interpretation
Der Inkreisradius ist das Verhältnis von Fläche zu halbem Umfang - eine fundamentale geometrische Beziehung.
Flächenzerlegung
Das Dreieck kann in drei kleinere Dreiecke zerlegt werden, deren Höhen alle gleich dem Inkreisradius sind.
Optimierung
Der Innenkreis maximiert die Kreisfläche bei gegebenem Dreieck - ein Optimierungsproblem.
Numerische Stabilität
Die Kombination von Heron-Formel und Inkreisberechnung ist numerisch robust.
Praktische Anwendungen
Innenkreis und Heron-Formel haben vielfältige praktische Anwendungen:
- Ingenieurswesen: Optimierung von Materialverwendung, größte einpassbare Rohre
- Computergrafik: Kollisionserkennung, Mesh-Optimierung, Textur-Mapping
- Architektur: Raumplanung, optimale Nutzung dreieckiger Flächen
- Vermessung: Flächenberechnung bei bekannten Seitenlängen
- Physik: Strömungsmechanik, Wärmeübertragung in dreieckigen Querschnitten
- Maschinenbau: Optimale Bohrungen, Materialersparnis
Mathematische Vertiefungen
Tangentenlängen
Die Tangentenlängen vom Eckpunkt zum Berührungspunkt können als s-a, s-b, s-c berechnet werden.
Beziehung zu anderen Kreisen
Umkreis und Inkreis stehen über die Euler-Beziehung R ≥ 2r in Verbindung.
Alternative Formeln
Es gibt verschiedene äquivalente Darstellungen der Heron-Formel für unterschiedliche Anwendungszwecke.
Verallgemeinerungen
Das Konzept lässt sich auf Polygone und höhere Dimensionen erweitern.
Spezialfälle und besondere Dreiecke
In verschiedenen Dreieckstypen zeigen sich besondere Eigenschaften:
- Gleichseitiges Dreieck: r = a/(2√3), maximaler Inkreisradius bei gegebenem Umfang
- Rechtwinkliges Dreieck: r = (a+b-c)/2, einfache Formel ohne Wurzel
- Gleichschenkliges Dreieck: Symmetrische Anordnung der Berührungspunkte
- Sehr spitze Dreiecke: Inkreis wird sehr klein, numerische Herausforderungen
Numerische Aspekte und Implementierung
Bei der praktischen Berechnung sind verschiedene Aspekte zu beachten:
Numerische Stabilität
Für sehr spitze oder sehr stumpfe Dreiecke können numerische Probleme auftreten.
Validierung
Die Dreiecksungleichung muss vor der Berechnung überprüft werden.
Alternative Algorithmen
Bei extremen Seitenverhältnissen können alternative Formeln stabiler sein.
Effizienz
Die Heron-Formel ist computationell effizient und gut parallelisierbar.
Zusammenfassung
Der Innenkreis eines Dreiecks und die Heron-Formel bilden ein perfektes Beispiel für die Eleganz der Geometrie. Sie verbinden praktische Anwendbarkeit mit mathematischer Schönheit und zeigen, wie antike Erkenntnisse auch in der modernen Mathematik und Technik von großer Bedeutung sind. Die einfache Beziehung r = A/s verkörpert die tiefe Verbindung zwischen verschiedenen geometrischen Eigenschaften eines Dreiecks.
|
|